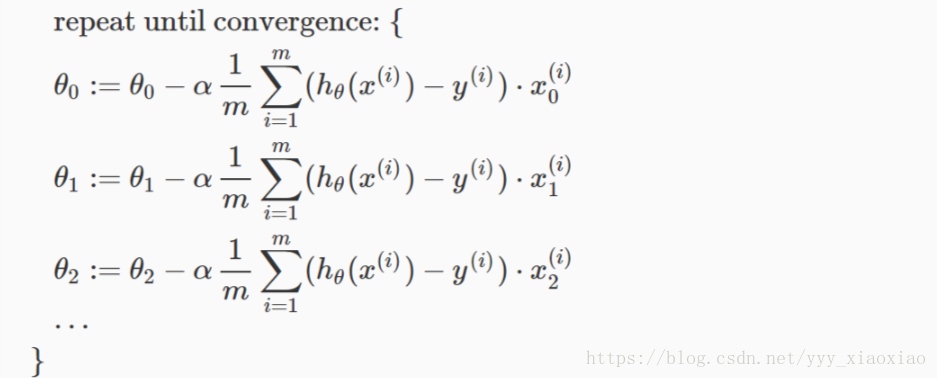机器学习部分算法
梯度下降和多线性回归
特征缩放
要对输入的m组data进行一个处理 将其放到一个矩阵中方便计算,或者对于不同范围的数据 进行特征缩放,规格化到[-1,1]或者比较接近这个范围
1
2
3
4
5
6
X_norm = X;
mu = zeros(1, size(X, 2));
sigma = zeros(1, size(X, 2));
mu=mean(X);
sigma=std(X);
X_norm = (X - repmat(mu,size(X,1),1)) ./ repmat(sigma,size(X,1),1);
1. 梯度下降
1
2
3
4
5
6
for iter = 1:num_iters
temp=((X*theta)-y)'*X;
theta=theta-alpha*(temp)'/m;
end
Cost Fuction
1
temp=(X*theta-y)'*(X*theta-y);
要同时更新,用temp储存,或者上面这种方法 利用导数进行进一步向min靠近
- 当偏导数为正数的时候,会减小;
- 当偏导数为负数的时候,会增加。
- 不论偏导数的符号如何,都会向最小值的方向运动。
- 每迭代一次,这项的值就会减小,因为随着越来越靠近最小值的过程中,偏导数那项会越来越小,直到趋近于零,或者小于10^-3;
- 当的初始值就为最小值的时候,迭代过程不做任何跟新
- 关于alpha的几点注意:
- 当X较小的时候,每次跟新的幅度就会比较小
- 当X较大的时候,可能会出现最后不收敛的情况
To summarize:
If α is too small: slow convergence.
If α is too large: may not decrease on every iteration and thus may not converge.
那如何来取我的alpha呢?
Make a plot with number of iterations on the x-axis.
我们可以看一个我们的J(0)这个函数的趋势,画出图像来看,或者有算法来判读。
2.多线性回归问题
Features
简单的理解一下,在一个问题里面一般会有多组变量 比如一个计算一个土地面积时有width 和 length 如果我们只是在做widtha和width^2的平方这样很复杂的去做,我们到的假设函数,反而不如我们把widthlength这样一个简单的假设函数
Polynomial Regression
简单的说就是一次函数不行,就要二次,三次函数等等 可能还是有很多种选择去符合我们的data。
正规分析
梯度下降给了我们一种很好的处理min的方式
还有一种就是正规分析

1
2
theta = zeros(size(X, 2), 1);
theta=inv(X'*X)*X'*y;
这种方式直接可以算出什么是最小的参数
比较这两种方式
比较直观的就是 正规分析更简单,但是对于大数据(100000)以上不适用 梯度下降比较复杂但是对于大量data会更好。