Search_度量方法调研与迁移学习

度量方法调研与迁移学习

1.理解迁移学习

重新理解我们的问题，我们目标也就是两个：在输出的feature map上度量时

同类之间的差距小，不同类之间的差距大
概率（准确率）高

在我们确定要去度量差距之后，我的重点就放在了度量方法的研究上。而刚好迁移学习的核心思想就是在做源域到目标域的迁移。通过度量两者之间的差距来调整或者finetune模型(上节组会还不知道这个名词，没想到在这遇见了)，而且我认为这些差距的度量其实就是在搞分布概率和数值差距来得到一个最优化目标。

跟传统的迁移学习相比，我们更关注数值差距问题。概率是结果

2. 度量方法调研

2.1 基本距离方法

欧式距离，衡量两个向量（空间上的点的距离）

由于feature map数值上太不靠谱，我们要用的话，可以进行GAP之后压缩的1维的标准化欧式距离。
马氏距离，有点像标准欧式距离，先将两个点投射到一个分布中，再加协方差，考虑方差

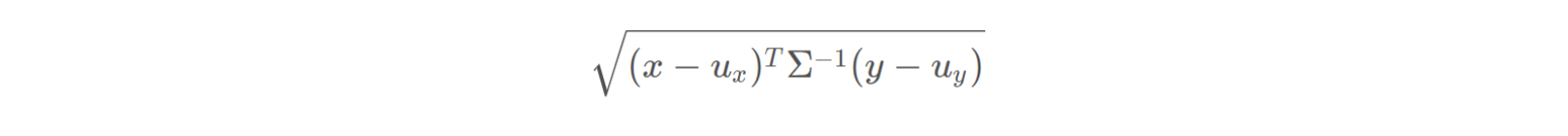
Σ 是这个分布的协方差。

最典型的就是根据距离作判别问题，即假设有n个总体，计算某个样品X归属于哪一类的问题。此时虽然样品X离某个总体的欧氏距离最近，但是未必归属它，比如该总体的方差很小，说明需要非常近才能归为该类。对于这种情况，马氏距离比欧氏距离更适合作判别。
余弦相似度，衡量两个向量的相关性 (夹角的余弦)。
互信息，定义在两个概率分布 X,Y 上，x ∈ X,y ∈ Y

2.2 流形学习

我们关注重点在数据上，那么这个feature map的多维数据怎么看出它的差距就是关键。

Grassmann 流形 G(d) 可以通过将原始的 d 维子空间 (特征向量) 看作它基础的元素，从而可以帮助学习分类器。在 Grassmann 流形中，特征变换和分布适配通常都有着有效的数值形式，因此在迁移学习问题中可以被很高效地表示和求解。因此，我感觉利用 Grassmann 流形空间中来进行处理也是可行的。

2.3 Maximum Mean Discrepancy

MMD最先提出的时候用于双样本的检测（two-sample test）问题，用于判断两个分布p和q是否相同。主要用来度量两个不同但相关的分布的距离。

最常用的场景就是domain adaption中衡量源域和目标域的距离。举个例子：深度迁移学习中网络就是一个函数,经过这个f(x)函数后，源域和目标域之间的差距越小，这个网络越能适用于目标域。

两个分布的距离定义为：

其中 H 表示这个距离是由\(ϕ() \)将数据映射到再生希尔伯特空间（RKHS）中进行度量的。

关于\(ϕ() \)函数，不同的分布可以取不同的值，但是大多数（DDC, DAN），都是用高斯核函数 \(k(u,v)=e{\frac{-∣∣u−v∣∣^2} {σ}} \) 来作为核函数。

因为\(ϕ()\)函数比较难定义，所以就之间展开来进行计算。

代码实践：

#!/usr/bin/env python
# encoding: utf-8

import torch
from torch.autograd import Variable

def guassian_kernel(source, target, kernel_mul=2.0, kernel_num=5, fix_sigma=None):
    n_samples = int(source.size()[0])+int(target.size()[0])
    total = torch.cat([source, target], dim=0)
    total0 = total.unsqueeze(0).expand(int(total.size(0)), int(total.size(0)), int(total.size(1)))
    total1 = total.unsqueeze(1).expand(int(total.size(0)), int(total.size(0)), int(total.size(1)))
    L2_distance = ((total0-total1)**2).sum(2)
    if fix_sigma:
        bandwidth = fix_sigma
    else:
        bandwidth = torch.sum(L2_distance.data) / (n_samples**2-n_samples)
    bandwidth /= kernel_mul ** (kernel_num // 2)
    bandwidth_list = [bandwidth * (kernel_mul**i) for i in range(kernel_num)]
    kernel_val = [torch.exp(-L2_distance / bandwidth_temp) for bandwidth_temp in bandwidth_list]
    return sum(kernel_val)#/len(kernel_val)

def mmd(source, target, kernel_mul=2.0, kernel_num=5, fix_sigma=None):
    batch_size = int(source.size()[0])
    kernels = guassian_kernel(source, target,
                              kernel_mul=kernel_mul, kernel_num=kernel_num,                    fix_sigma=fix_sigma)
    XX = kernels[:batch_size, :batch_size]
    YY = kernels[batch_size:, batch_size:]
    XY = kernels[:batch_size, batch_size:]
    YX = kernels[batch_size:, :batch_size]
    loss = torch.mean(XX + YY - XY -YX)
    return loss

随机random生成两个不同的分布，随机取10*500对应值去计算一下，然后相同分布计算值为0.7，不同分布计算值7.4。虽然对内部的信息还有又不知道的地方，但是已经可以直观看出MMD判断差距的能力。

也可以用于度量两个分布的相似性：如果对于所有以分布生成的样本空间为输入的函数f，如果两个分布生成的足够多的样本在f上的对应的像的均值都相等，那么那么可以认为这两个分布是同一个分布。、

3. 深度学习与迁移学习

3.1 DCC

先看这个图吧，这是在两个不同的训练集上面进行迁移学习。而且使用loss的方法对两个网络fc的output array 进行惩罚来学习，不就是我们的第二种3.2事中学习的思想吗？对两个数据来进行比较。他们是两类，我们是一组（多个）。

DDC 方法 (Deep Domain Confusion) 解决深度网络的自适应问题。DDC 固定了 AlexNet 的前 7 层，在第 8 层 (分类器前一层) 上加入了自适应的度量。自适应度量方法采用了被广泛使用的 MMD 准则。DDC 方法的损失函数表示为：

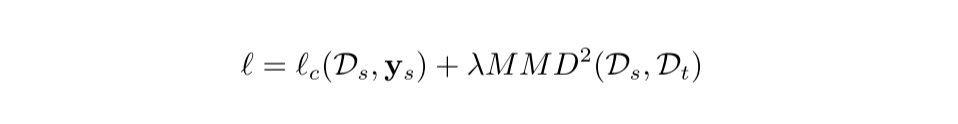
3.2 DAN

DAN 方法 (Deep Adaptation Networks) 对 DDC 方法进行了几个方面的扩展。

有别于 DDC 方法只加入一个自适应层，DAN 方法同时加入了三个自适应层 (分类器前三层)。
DAN方法采用了表征能力更好的多核MMD度量(MK-MMD代替了 DDC 方法中的单一核 MMD。
DAN 方法将多核 MMD 的参数学习融入到深度网络的训练中，不增加网络的额外训练时间。DAN 方法在多个任务上都取得了比 DDC 更好的分类效果。

也使用了t-she降维和对比了DDC和DAN的差距

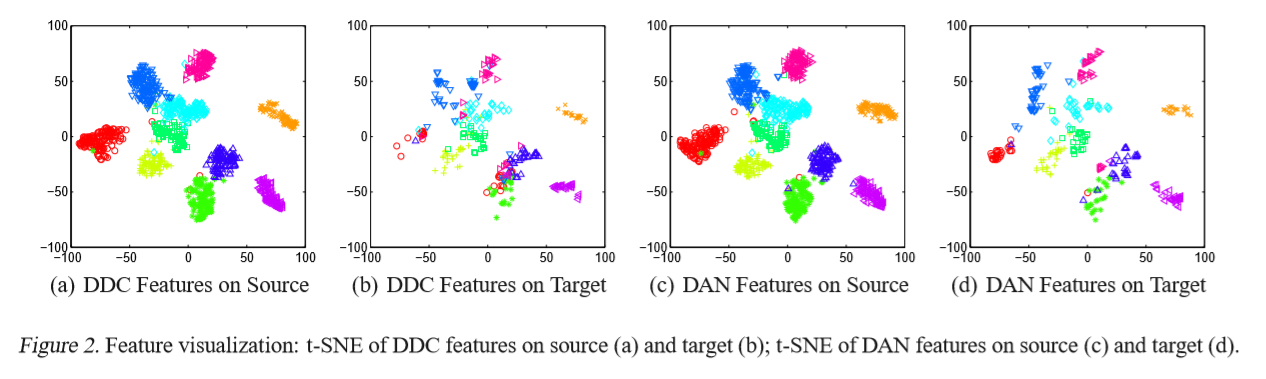
大致看了看这两篇论文，后面找时间再拜读。

Learning Transferable Features with Deep Adaptation Networks

DeepDomainConfusion: MaximizingforDomainInvariance

4. 总结

事后解释性，引用迁移学习中的MMD方法来度量差距，可以先对一部分数据进行MMD差距看看结果。
针对上一点，有一个不同点就是我们类会有很多，不一定每一个都好
事中解释性，我们可以对input和output上加MMD loss来惩罚网络。优点：输入不变，可以比较好训练
或者是对两个不同类别的output来MMD loss来训练。优点：都在feature map上维度一致。

最后回扣到我们的最初的解释性，feature map resize到原图大小后，可以只对比location 位置的像素。这样不就是可以满足我们最初的目标：在即分类和定位的网络上解释

5.future work

进一步了解度量方法，学习度量学习 MML
总结和思考目前进展中的问题

5.1 Question Lists

5.1.1 针对事后解释性

在feature map 度量距离的函数应该用什么方法确定？是否考虑此算法的普适性？即针对不同类的数据都可以直接拿来对比，还是说要进行一定针对性的pre-train。
如果是选择经过针对性预训练的核函数，利用什么数据进行预训练？label数据集？这样做会不会带来新的训练难题？已经这个核函数是不是可解释的，用一个不可解释的方法去解释另一个不可解释的，显然是有新问题出现的。
核心思想数据对比，如何进行。是在input和output之间，还是在两个output之间（都能说通）。
数据对比是针对全局还是像CAM那样对局部范围进行对比，或者之间利用数据的位置标签（x,y,h,w）
feature map位置以及维度的选择？

5.1.2 针对事中解释性

loss函数的选择，triplet loss，N-mc loss ，是否考虑angle信息，以及如何和网络的原来的loss进行结合？
loss是加到总loss上面进行训练，还是针对输出feature map的那一层的filter？
是通过output和input之间的差距来训练网络，还是使用output和output的差距进行训练?或者也可以两者进行结合。loss由三部分组成？
这种事中解释性，显然让我们的网络的解释性变得更复杂了，更难说清楚了。只通过最先想法，综述文章中的那一个衡量可解释性的性质，是不是会显得不够有力度。是不是要再加一些去支撑。还是说先做到自圆其说。
尽量能够保证我们端到端的网络构想。