4.18 机器学习与认知计算所第四次组会问题记录
1.统计方法设计
根据层次聚类算法,进行有统计意义的计算
会议上,老师对我的实验结果进行了质疑,以前没接触过对应的聚类统计方法,在上一次设计实验时,并没有考虑到实验的随机性,缺乏这方面的知识。刚好亡羊补牢在此进行针对性的学习。
1.1 任务明细
上次实验,我们将mnist在cam中gap层的数据进行了导出,得到了一个 300x64x10 的矩阵 , 这相当于是一个根据标签分类好的数据集。
我们现在要实现对每个簇两两之间差距的度量,得到一个可信的值。batch_size 可以有多种选择
1.2 方法明确
Single-linkage:要比较的距离为元素对之间的最小距离
Complete-linkage:要比较的距离为元素对之间的最大距离
Group average:要比较的距离为类之间的平均距离(平均距离的定义与计算:假设有A,B两个类,A中有n个元素,B中有m个元素。在A与B中各取一个元素,可得到他们之间的距离。将nm个这样的距离相加,得到距离和。最后距离和除以nm得到A,B两个类的平均距离。
2.类中心计算
根据统计方法进行类中心的计算,也可以局部化去研究更好的类中心
由于我们已经知道对应的数据的类别,就不要再给10类的数据进行训练了
所有直接给每一类进行一个k-means算法,来获得这个类的类中心
k-means算法进行迭代运算的是欧式距离,我们可以用MMD或者其他距离计算公式来迭代计算
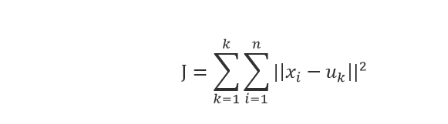
3. 计算类中心和输入样本之间的差距
然后来影响feature map 上面的参数,进行反回,影响热力图的生成
目前的想法就是对输入样本经过计算后的值,和类中心进行度量距离,如果距离很小,说明很近,返回要加强,如果距离很小,返回要减少
- 计算到问题之后,是否直接给返回乘以一个系数
- 或者对应的每个位置都进行一个细粒度的划分
个人认为,如果乘以一个系数这种方法虽然粗犷,但是应该会有比较好的结果