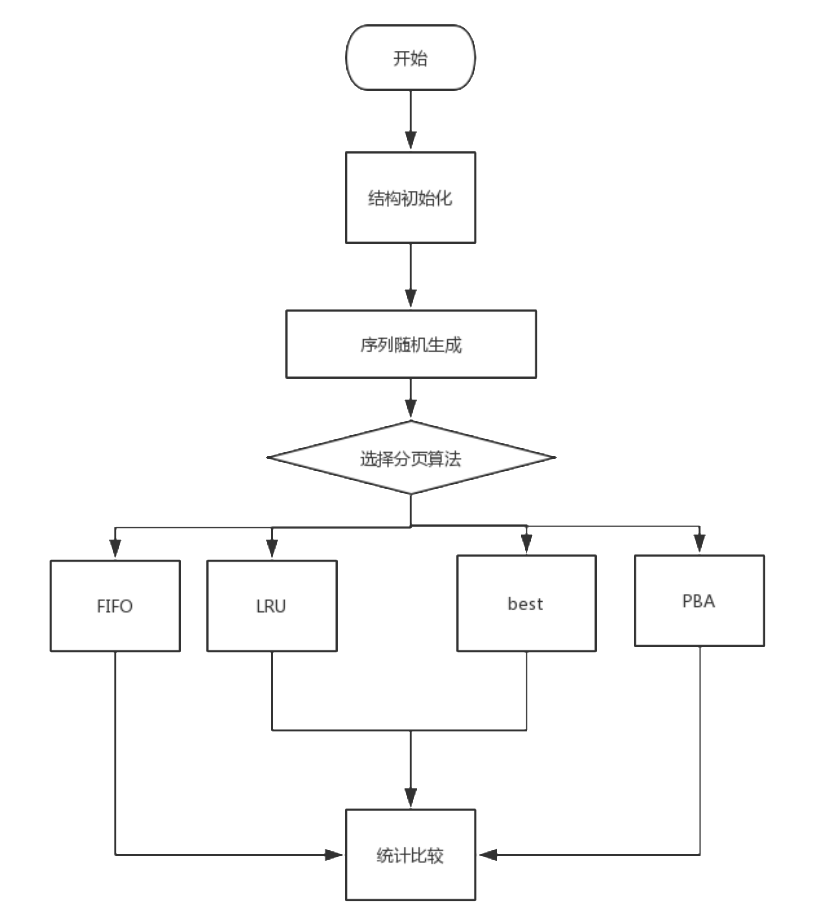
操作系统实验四 页面置换算法
“16281052 杨涵晨 计科1601 ”
github 地址 https://github.com/neoyanghc/2019_BJTU_OS_16281052/tree/master/lab4
实验目的
设计和实现
- 最佳置换算法
- 先进先出置换算法
- 最近最久未使用置换算法
- 页面缓冲置换算法
通过模拟指令集,来实现对各种算法性能的计算与对比。
实验概要设计
经过对此实验的分析,可以对实验进行前期的分析和调查。
- 完成虚拟页面结构的设计
- 页面结构体的设计
- 页表项中数据如何存储设计,以及结构体的实现
- 随机访问序列的设计
- 编写函数实现
- 4种算法的设计与实现
- 最佳置换算法
- 先进先出置换算法
- 最近最久未使用置换算法
- 页面缓冲置换算法
- 性能对比与分析
- 进行多次实验
- 系统展示函数设计
- 对用户提供一些展示

本实验将主要包含4个模块
-
页面结构设计模块
主要是对虚拟页面的结构进行定义,方便后面的存储和调用
-
随机序列生成模块
编写generate函数,返回生成好的序列信息。
-
算法实现模块
编写4种算法调用函数,直接供主程序进行选择调用,输入为生成的序列,输出为各种统计信息
-
统计对比模块
收集存储各种算法的统计信息,对其进行比对。

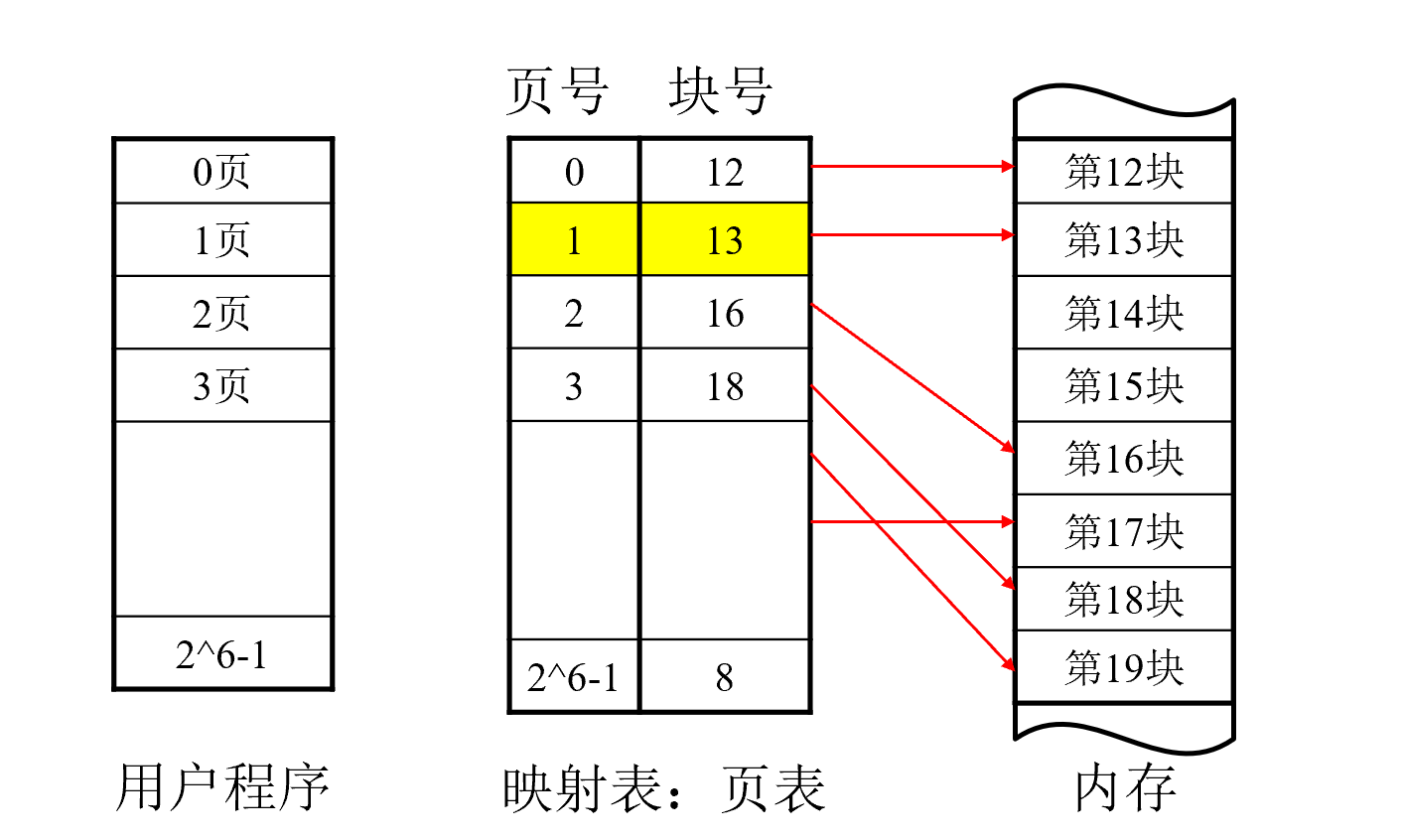
Task 1 页面结构设计
由于,模拟的虚拟内存的地址为16位,页面大小为1K

首先16位的虚拟地址可表示的进程大小应该是2^16B = 64KB
根据页的定义和页面大小的定义将进程进行分页:
\[页面的大小=\frac{进程的大小}{页面的大小}=\frac{逻辑地址表示的大小}{页面的大小}=\frac{2^{16B}}{1KB}=2^{6}页\]所有一共有$2^{6}个物理块$,所以页号p=6
偏移量为16-6=10位,所以p=6,w=10
所以页面需要$2^{6}*2B=128B$的内存存储
编写c语言程序实现页面结构设计
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
struct PageInfo //页面信息结构
{
int data[MAX]; // 模拟的最大访问页面数,16位信息,前6位代表页号,后10位为偏移地址 0~2^16
int flag; // 标志位,0表示无页面访问数据
int unfind; // 统计信息,缺页次数,缺页中断次数
int size; // 分配的页框数
int length; // 访问页面序列长度
} page_info;
struct memoryInfo
{
int flag;//访问位
int modify;//修改位
int data;//页号,16位信息,前6位代表页号,后10位为偏移地址 0~2^16
int time;
}
Task2 随机序列生成
根据给出的随机序列生成思想,进行编写
- 确定虚拟内存的尺寸N,工作集的起始位置p,工作集中包含的页数e,工作集移动率m(每处理m个页面访问则将起始位置p +1),
- 以及一个范围在0和1之间的值t;
- 生成m个取值范围在p和p + e间的随机数,并记录到页面访问序列串中;
- 生成一个随机数r,0 ≤ r ≤ 1;如果r < t,则为p生成一个新值,否则p = (p + 1) mod N;
- 如果想继续加大页面访问序列串的长度,请返回第2步,否则结束。
编写函数实现序列生成函数,输入函数为工作集移动率m,工作集中包含的页数e,重复次数s.
函数如下void generate(int m,int e,int s)
将存入的序列放入data数组中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
void generate(int m,int e,int s)
{
int pn,i, j=0;
init(); //初始化相关数据结构
printf("\n请输入要随机生成访问序列的长度:"); //自定义随机生成访问序列的长度
scanf("%d", &pn);
page_info.length = pn;
srand((unsigned)time(NULL)); //用时间做种,每次产生随机数不一样
int p = rand() % MAX;
double t;
t = rand() % 10 / 10.0; // 0-1之间的数
//如果想继续加大页面访问序列串的长度,请返回第2步,否则结束。
for (i = 0; i < s; i++)
{
if (j > page_info.length)
break;
//生成m个取值范围在p和p + e间的随机数,并记录到页面访问序列串中;
for (j = i * m; j < (i + 1) * m; j++)
{
page_info.data[j]= (p + (rand() % e)) % MAX;
}
// 生成一个随机数r,0 ≤ r ≤ 1;
double r = (rand() % 10) / 10.0;
// 如果r < t,则为p生成一个新值
if (r < t)
{
p = rand() % MAX;
}
//否则p = (p + 1) mod N;
else
{
p = (p + 1) % MAX;
}
}
}
当 m = 8, e=8时,对应的随机访问序列:
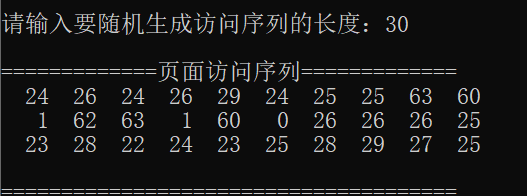
Task3 最佳置换算法OPT
主要思想:
- 从主存中移出永远不再需要的页面;
- 如无这样的页面存在,则选择最长时间不需要访问的页面。
于是,所选择的被淘汰页面将是以后永不使用的,或者是在最长时间内不再被访问的页面,这样可以保证获得最低的缺页率。
假定系统为某进程分配了三个物理块,并考虑有以下页面号引用串: 7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2, 1, 2, 0, 1, 7, 0, 1 进程运行时,先将7, 0, 1三个页面依次装入内存。进程要访问页面2时,产生缺页中断,根据最佳置换算法,选择第18次访问才需调入的页面7予以淘汰。然后,访问页面0时,因为已在内存中所以不必产生缺页中断。访问页面3时又会根据最佳置换算法将页面1淘汰……依此类推
| 页面 | 7 | 0 | 1 | 2 | 0 | 3 | 0 | 4 | 2 | 3 | 0 | 3 | 2 | 1 | 2 | 0 | 1 | 7 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 页面1 | 7 | 7 | 7 | 2 | 2 | 2 | 2 | 2 | 7 | |||||||||||
| 页面2 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | ||||||||||||
| 页面3 | 1 | 1 | 3 | 3 | 3 | 1 | 1 | |||||||||||||
| 缺页 | √ | √ | √ | √ | √ | √ | √ | √ |
编写代码实现OPT函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
void OPT()
{
int n, full, status;
change_page = 0; // 页面替换指针初始化为0
loss = 0; // 缺页数初始化为0
generate(); // 随机生成访问序列
full = 0; // 是否装满是所有的页框
for (n = 0; n < page_info.size; n++) // 清除页框信息
{
page_list[n] = -1;
}
flag_of_page = 0; //缺页标志,0为不缺页,1为缺页
for (current_page = 0; current_page < page_info.length; current_page++) //执行算法
{
status = find_page(page_info.data[current_page]); //查找页面是否在内存
if (full < page_info.size) // 开始时不计算缺页
{
if (status == 0) // 页不存在则装入页面
{
page_list[change_page] = page_info.data[current_page];
change_page = (change_page + 1) % page_info.size;
full++;
}
}
else // 正常缺页置换
{
if (status == 0) // 页不存在则置换页面
{
int min,max = 0 ; //很大的数
for (int m = 0; m < page_info.size ;m++)
{
min = 1000;
for (int n = current_page; n < page_info.length; n++)
{
if (page_info.data[n] == page_list[m])
{
min = n;
break;
}
}
if (max < min)
{
max = min;
change_page = m;
}
}
page_list[change_page] = page_info.data[current_page];
change_page = (change_page + 1) % page_info.size;
page_info.unfind++; // 缺页次数加1
}
}
Sleep(10);
display(); // 显示当前状态
} // 置换算法循环结束
return;
}
执行结果
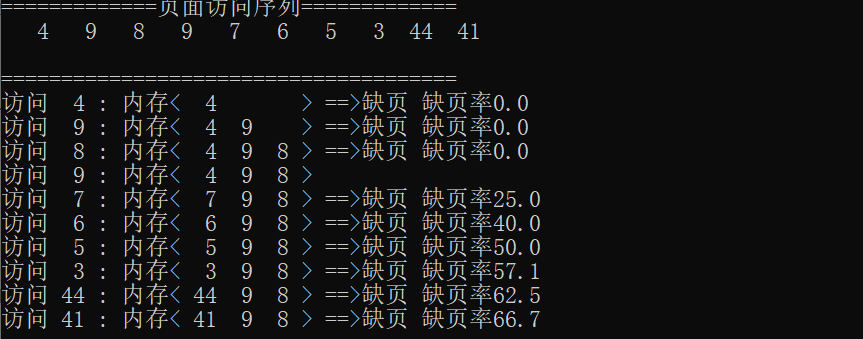
Task4 FIFO算法
这种算法并不难,主要思想是:当需要淘汰一个页面时,总是选择驻留主存时间最长的页面进行淘汰,即先进入主存的页面先淘汰。其理由是:最早调入主存的页面不再被使用的可能性最大。
| 页面 | 7 | 0 | 1 | 2 | 0 | 3 | 0 | 4 | 2 | 3 | 0 | 3 | 2 | 1 | 2 | 0 | 1 | 7 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 页面1 | 7 | 7 | 7 | 2 | 2 | 2 | 4 | 4 | 4 | 0 | 0 | 0 | 7 | 7 | 7 | |||||
| 页面2 | 0 | 0 | 0 | 3 | 3 | 3 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | ||||||
| 页面3 | 1 | 1 | 1 | 0 | 0 | 0 | 3 | 3 | 3 | 2 | 2 | 2 | 1 | |||||||
| 缺页 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
这里仍用上面的实例,釆用FIFO算法进行页面置换。进程访问页面2时,把最早进入内存的页面7换出。然后访问页面3时,再把2, 0, 1中最先进入内存的页换出。可以看出,利用FIFO算法时进行了 12次页面置换,比最佳置换算法正好多一倍。
FIFO算法基于队列实现,这里我们用数组模拟队列实现。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
void FIFO(void)
{
int n, full, status;
change_page = 0; // 页面替换指针初始化为0
loss = 0; // 缺页数初始化为0
generate(); // 随机生成访问序列
full = 0; // 是否装满是所有的页框
for (n = 0; n < page_info.size; n++) // 清除页框信息
{
page_list[n] = -1;
}
flag_of_page = 0; //缺页标志,0为不缺页,1为缺页
for (current_page = 0; current_page < page_info.length; current_page++) //执行算法
{
status = find_page(page_info.data[current_page]); //查找页面是否在内存
if (full < page_info.size) // 开始时不计算缺页
{
if (status == 0) // 页不存在则装入页面
{
page_list[change_page] = page_info.data[current_page];
change_page = (change_page + 1) % page_info.size;
full++;
}
}
else // 正常缺页置换
{
if (status == 0) // 页不存在则置换页面
{
page_list[change_page] = page_info.data[current_page];
change_page = (change_page + 1) % page_info.size;
page_info.unfind++; // 缺页次数加1
}
}
Sleep(10);
display(); // 显示当前状态
} // 置换算法循环结束
return;
}
执行结果
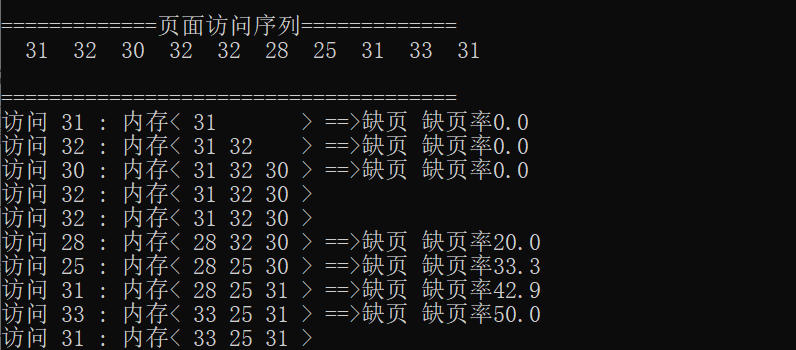
Task5 最近最久未使用LRU
这种算法的基本思想是:利用局部性原理,根据一个作业在执行过程中过去的页面访问历史来推测未来的行为。它认为过去一段时间里不曾被访问过的页面,在最近的将来可能也不会再被访问。所以,这种算法的实质是:当需要淘汰一个页面时,总是选择在最近一段时间内最久不用的页面予以淘汰。
| 页面 | 7 | 0 | 1 | 2 | 0 | 3 | 0 | 4 | 2 | 3 | 0 | 3 | 2 | 1 | 2 | 0 | 1 | 7 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 页面1 | 7 | 7 | 7 | 2 | 2 | 4 | 4 | 4 | 0 | 1 | 1 | 1 | ||||||||
| 页面2 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 3 | 0 | 0 | |||||||||
| 页面3 | 1 | 1 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 7 | ||||||||||
| 缺页 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
再对上面的实例釆用LRU算法进行页面置换。进程第一次对页面2访问时,将最近最久未被访问的页面7置换出去。然后访问页面3时,将最近最久未使用的页面1换出。
实际上,LRU算法根据各页以前的情况,是“向前看”的,而最佳置换算法则根据各页以后的使用情况,是“向后看”的。
LRU是堆栈类的算法
利用page_history数组,存储当前页面调用的距离时间time。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// LRU页面置换算法
void LRU(void)
{
int n, full, status, max;
change_page = 0; // 页面替换指针
loss = 0; // 缺页次数初始化为0
generate(); // 随机生成访问序列
full = 0; // 是否装满所有的页框
for (n = 0; n < page_info.size; n++)
{
page_list[n] = -1; // 清除页框信息
page_history[n] = 0; // 清除页框历史
}
flag_of_page = 0; //缺页标志,0为不缺页,1为缺页
for (current_page = 0; current_page < page_info.length; current_page++) // 执行算法
{
status = find_page(page_info.data[current_page]); //查找页面是否在内存
if (full < page_info.size) // 开始时不计算缺页
{
if (status == 0) // 页不存在则装入页面
{
page_list[change_page] = page_info.data[current_page];
//把要调入的页面放入一个空的页框里
change_page = (change_page + 1) % page_info.size;
full++;
}
}
else //正常缺页置换
{
if (status == 0)//页不存在则置换页面
{
max = 0;
for (n = 1; n < page_info.size; n++)
{
if (page_history[n] > page_history[max])
{
max = n;
}
}
change_page = max;
page_list[change_page] = page_info.data[current_page];
page_history[change_page] = 0;
page_info.unfind++; // 缺页次数加1
}
}
Sleep(10);
display(); // 显示当前状态
} // 置换算法循环结束
_getch();
return;
}
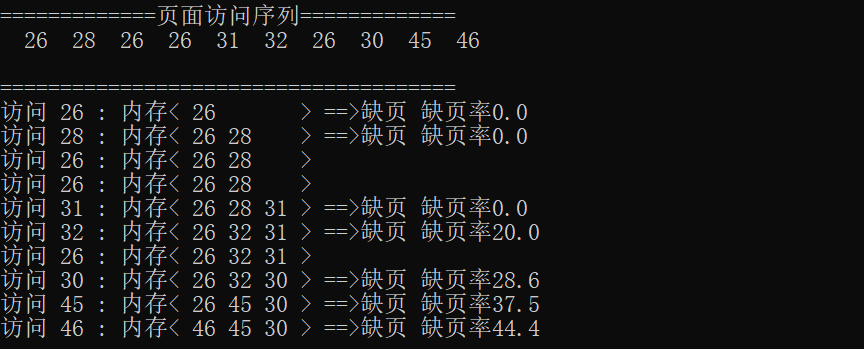
结果如下:
Task6 改进型Clock置换算法
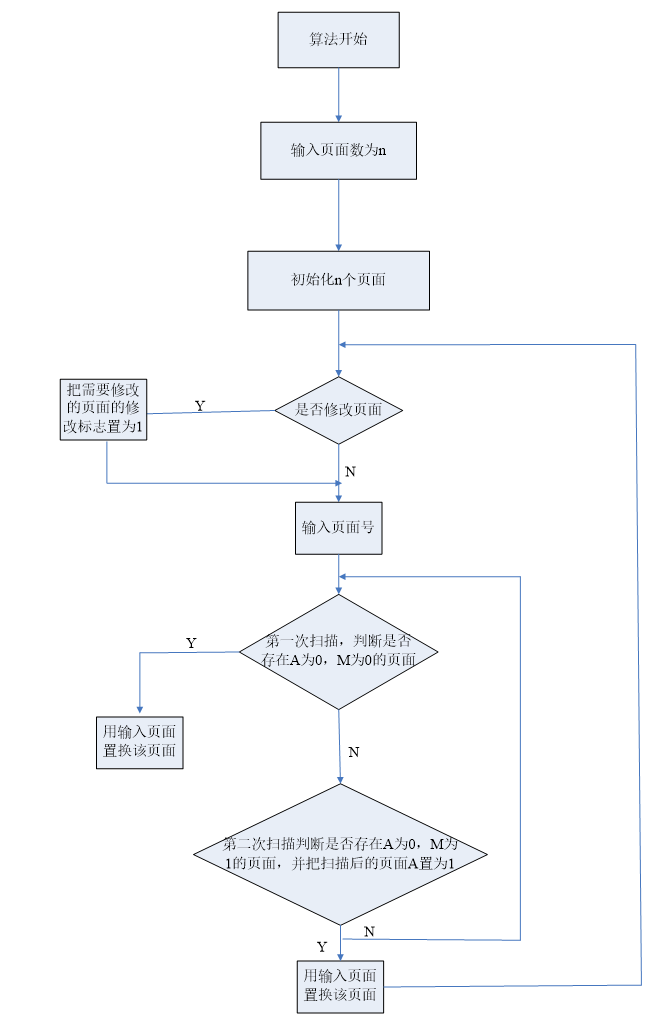
主要思想是,在每次页面替换时,总是尽可能地先替换掉既未被访问又未被修改的页面。
改进型的CLOCK置换算法种,每一帧都处于以下四种情况之一:
- 最近未被访问,也未被修改(u=0, m=0)。
- 最近被访问,但未被修改(u=1, m=0)。
- 最近未被访问,但被修改(u=0, m=1)。
- 最近被访问,被修改(u=1, m=1)。
算法执行如下操作步骤:
- 从指针的当前位置开始,扫描帧缓冲区。在这次扫描过程中,对使用位不做任何修改。选择遇到的第一个帧(u=0, m=0)用于替换。
- 如果第1)步失败,则重新扫描,查找(u=0, m=1)的帧。选择遇到的第一个这样的帧用于替换。在这个扫描过程中,对每个跳过的帧,把它的使用位设置成0。
- 如果第2)步失败,指针将回到它的最初位置,并且集合中所有帧的使用位均为0。重复第1步,并且如果有必要,重复第2步。这样将可以找到供替换的帧。
算法流程如下所示:
编写代码如下所示:其中change()函数是一个随机函数,负责对应的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//查找替换页面算法,递归实现
int whichpage(int num) {
int j;
for (j = 0; j < page_info.size; j++)
{
if (page_list[(j + num) % page_info.size].A == 0 && page_list[(j+num)%page_info.size].M == 0)
{
return (j+num)%page_info.size;
}
}
for (j = 0; j < page_info.size; j++)
{
if (page_list[(j + num) % page_info.size].A == 0 && page_list[(j + num) % page_info.size].M == 1)
{
return (j + num) % page_info.size;
}
page_list[(j + num) % page_info.size].A = 0;
}
for (j = 0; j < page_info.size; (j+num)%page_info.size++)
{
page_list[(j + num) % page_info.size].A = 0;
}
return whichpage(num);
}
改进的clock算法,调用其他函数完成页面置换操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
void CLOCK()
{
int n, full, status;
change_page = 0; // 页面替换指针初始化为0
loss = 0; // 缺页数初始化为0
generate(); // 随机生成访问序列
full = 0; // 是否装满是所有的页框
for (n = 0; n < page_info.size; n++) // 清除页框信息
{
page_list[n].data = -1;
page_list[n].M = 0;
page_list[n].A = 0;
page_list[n].time = 0;
}
flag_of_page = 0; //缺页标志,0为不缺页,1为缺页
for (current_page = 0; current_page < page_info.length; current_page++) // 执行算法
{
status = find_page(page_info.data[current_page]); //查找页面是否在内存
if (full < page_info.size) // 开始时不计算缺页
{
if (status == 0) // 页不存在则装入页面
{
page_list[change_page].data = page_info.data[current_page];
page_list[n].A = 1;
full++;
}
}
else // 正常缺页置换
{
if (status == 0) // 页不存在则置换页面
{
change_page = whichpage();
page_list[change_page].data = page_info.data[current_page];
page_list[change_page].A = 1;
page_info.unfind++; // 缺页次数加1
}
}
Sleep(10);
display(); // 显示当前状态
} // 置换算法循环结束
_getch();
return;
}
执行结果

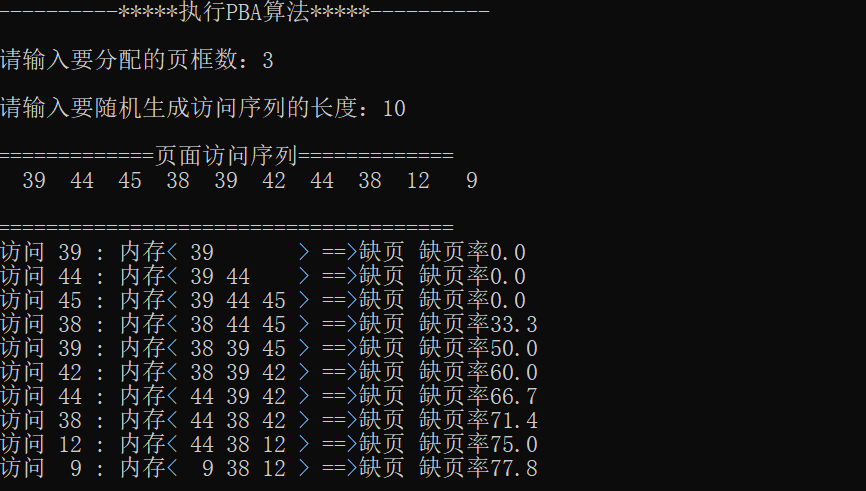
Task7 PBA页面缓存算法
主要思想:利用二级队列,存储当前不使用页面的信息,当缺页发生时,会查找二级队列,从二级队列中直接写入页表中,降低取页面的时间。
设立空闲页面链表和已修改页面链表采用可变分配和基于先进先出的局部置换策略,并规定被淘汰页先不做物理移动,而是依据是否修改分别挂到空闲页面链表或已修改页面链表的末尾,空闲页面链表同时用于物理块分配,当已修改页面链表达到一定长度如Z个页面时,一起将所有已修改页面写回磁盘,故可显著减少磁盘I/O操作次数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
void PBA()
{
int n, full, status;
change_page = 0; // 页面替换指针初始化为0
loss = 0; // 缺页数初始化为0
memoryInfo page_buffer[MAX]; // 分配的页框
generate(); // 随机生成访问序列
full = 0; // 是否装满是所有的页框
for (n = 0; n < page_info.size; n++) // 清除页框信息
{
page_list[n].data = -1;
page_buffer[n].data = -1; // 缓冲链表
}
flag_of_page = 0; //缺页标志,0为不缺页,1为缺页
for (current_page = 0; current_page < page_info.length; current_page++) // 执行算法
{
status = find_page(page_info.data[current_page]); //查找页面是否在内存
if (full < page_info.size) // 开始时不计算缺页
{
if (status == 0) // 页不存在则装入页面
{
page_list[change_page].data = page_info.data[current_page];
change_page = (change_page + 1) % page_info.size;
full++;
}
}
else // 正常缺页置换
{
if (status == 0) // 页不存在则置换页面
{
int num = 0;
//page_buffer[num++] = page_list[change_page]; //添加到buffer中
page_buffer(change_number); //查看buffer二级队列中是否存在
change_buffer(); //对队列进行操作
page_list[change_page].data = page_info.data[current_page];
change_page = (change_page + 1) % page_info.size;
page_info.unfind++; // 缺页次数加1
}
}
Sleep(10);
display(); // 显示当前状态
} // 置换算法循环结束
return;
}
执行结果
Task 8 算法对比和总结
我们对每一中算法进行缺页率的计算和对比,我们将页框数从3-20进行了模拟。
1. 命中率对比
随机生成序列长度设定在50,来计算命中率。得到的表如下所示。
| 页框数 | OPT命中率 | FIFO命中率 | LRU命中率 | CLOCK命中率 | PBA命中率 |
|---|---|---|---|---|---|
| 3 | 0.6425 | 0.5275 | 0.5275 | 0.5250 | 0.5275 |
| 4 | 0.6675 | 0.5425 | 0.5375 | 0.5300 | 0.5425 |
| 5 | 0.6900 | 0.5475 | 0.5475 | 0.5425 | 0.5475 |
| 6 | 0.7100 | 0.5500 | 0.5625 | 0.5625 | 0.5500 |
| 7 | 0.7275 | 0.5725 | 0.5800 | 0.5800 | 0.5725 |
| 8 | 0.7450 | 0.5725 | 0.5875 | 0.6050 | 0.5725 |
| 9 | 0.7600 | 0.6050 | 0.6000 | 0.6100 | 0.6050 |
| 10 | 0.7750 | 0.6225 | 0.6250 | 0.6200 | 0.6225 |
| 11 | 0.7900 | 0.6325 | 0.6375 | 0.6275 | 0.6325 |
| 12 | 0.8050 | 0.6425 | 0.6450 | 0.6425 | 0.6425 |
| 13 | 0.8175 | 0.6600 | 0.6525 | 0.6675 | 0.6600 |
| 14 | 0.8300 | 0.6725 | 0.6725 | 0.6825 | 0.6725 |
| 15 | 0.8425 | 0.6850 | 0.6950 | 0.6975 | 0.6850 |
| 16 | 0.8675 | 0.7175 | 0.7300 | 0.7225 | 0.7175 |
| 17 | 0.8775 | 0.7525 | 0.7350 | 0.7525 | 0.7525 |
| 18 | 0.8875 | 0.7600 | 0.7525 | 0.7700 | 0.7600 |
| 19 | 0.8975 | 0.7625 | 0.7600 | 0.8250 | 0.7625 |
| 20 | 0.9225 | 0.8250 | 0.8050 | 0.8400 | 0.8250 |
总的来看:性能(缺页率)如下。
最佳置换算法 > 改进型clock置换算法 > 最近最久未使用算法 >= 先进先出置换算法 = PBA算法
- 最佳置换算法的缺页率是最低的,这一点是毋庸置疑的。
- 改进型clock算法稍微好于先进先出算法和最近最久未使用算法。
- 先进先出算法和最近最久未使用算法性能相近
- PBA算法和先进先出算法相似,这是因为PBA只会降低调取访问时间,不影响缺页率·。
还可以发现,算法的缺页率还跟分配的内存块数有关系,分配的内存块数越多,缺页率越低。这与直观感受是一致的,即导入内存的块数越多,发生缺页的可能性就越小。
2. 算法开销对比
随机生成序列长度设定在50,来计算花费时间, 如下所示。
| 页框数 | OPT时间() | FIFO时间 | LRU时间 | CLOCK时间 | PBA时间 |
|---|---|---|---|---|---|
| 3 | 6.609 | 2.230 | 3.005 | 5.280 | 7.562 |
| 4 | 12.05 | 3.025 | 7.560 | 6.230 | 13.02 |
| 5 | 30.20 | 5.203 | 5.202 | 13.05 | 15.36 |
总体来看是。
先进先出置换算法 < 最近最久未使用算法 < 改进型clock置换算法 < 最佳置换算法 = = PBA算法
- 先进先出算法的计算时间最小,算法效率最高
- OPT相对来说是最差的
- PBA算法差的原因可能是由于存在为此两个链表的开销太大。但是实际中应该好于最佳置换算法