Leetcode刷题问题记录与解答

1. 目前进度

每天差不多刷4道题，然后已经坚持了两周了。还有两周要继续加油！

2.难点题目分析与解答

2.1 哈希表

哈希表在查找元素是否存在时，有天然的优势，它通过键值映射维持一个散列结构。并且以红黑树的形式存储

查找速度很快。当我们需要对应元素查找时，哈希表应该首先被我们考虑

1.Two Sum

这道题其实就是典型的查找问题，希望两数之和等于target 其实就是相当于：存在一个数a，同时也存在一个数target - a。因此我们就可以利用hashmap进行查找。即将一个数a放入hashmap的同时，查找target-a的值

如果存在，停止循环返回True

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        map<int,int> a;//提供一对一的hash
        vector<int> b(2,-1);//用来承载结果，初始化一个大小为2，值为-1的容器b
        for(int i=0;i<nums.size();i++)
        {
            if(a.count(target-nums[i])>0)
            {
                b[0]=a[target-nums[i]];
                b[1]=i;
                break;
            }
            a[nums[i]]=i;//反过来放入map中，用来获取结果下标
        }
        return b;
    };
};

# python 使用一个字典进行映射，底层也是hashmap吧
class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        _dict = {}
        # 这里也可以使用range，enumerate不是很常用
        for i, m in enumerate(nums):
            if _dict.get(target - m) is not None:
                return [_dict.get(target - m),i]
            _dict[m] = i

2.字母异位分组

通过以”单词的字典序“为映射标准，来进行实现

每当一个单词进入时，将其分割然后对其进行sort()排序，根据键值加入到map中

class Solution(object):
    def groupAnagrams(self, strs):
        # 这里的defaultdict 其实是初始化一个dict,不然当一个新key值进入时会出现keyerror
        ans = collections.defaultdict(list)
        for s in strs:
            ans[tuple(sorted(s))].append(s)
        return ans.values()

2.2 滑动窗口

1.最小覆盖子串

首先，子串和子序列是不同的，子串必须时连续的，连续的也就可以想到滑动窗口sliding windows

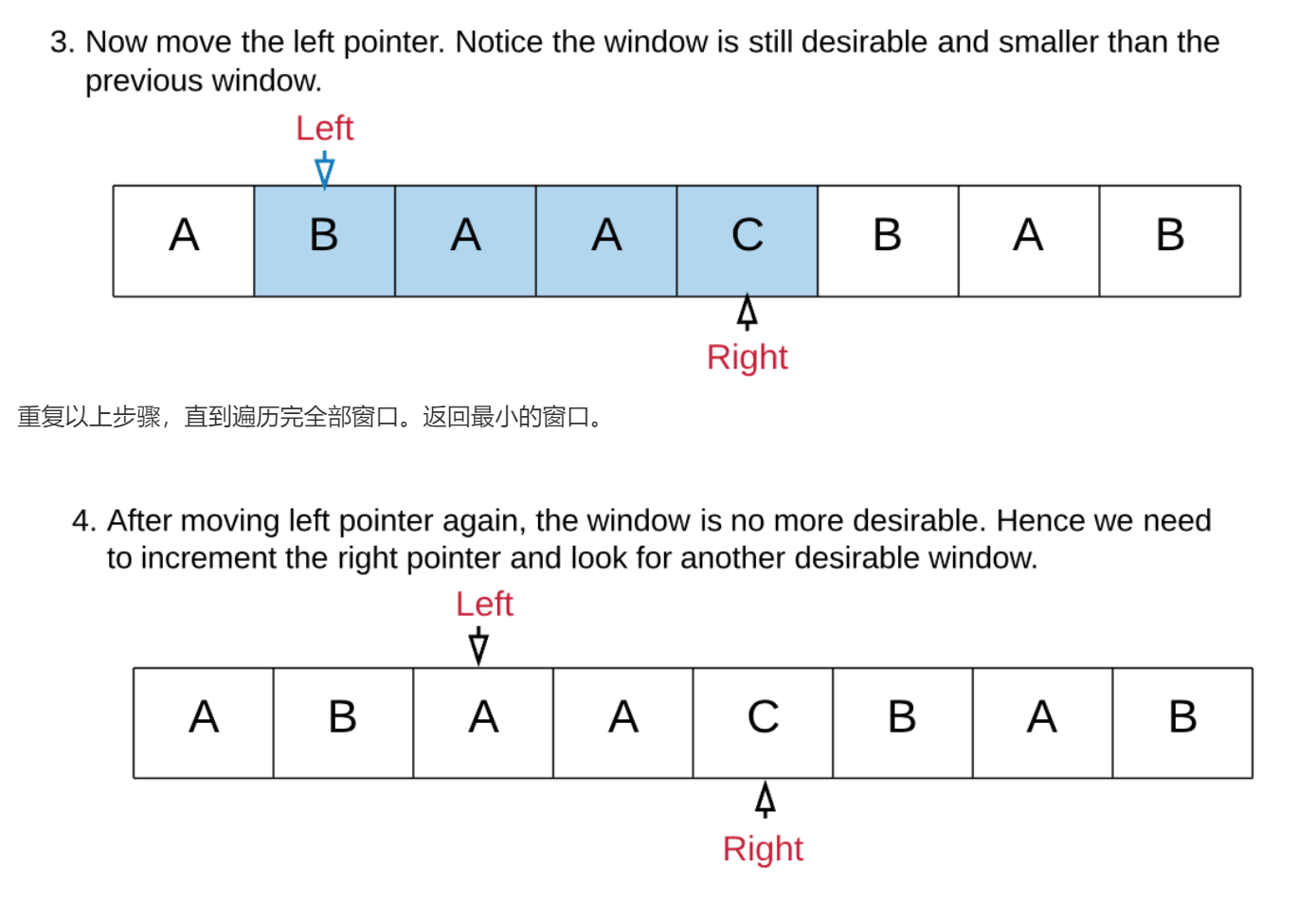
然后我们使用

def minWindow(self, s, t):
    if not t or not s:
        return ""

    # 对t中的元素进行计数，并返回一个list
    dict_t = Counter(t)

    required = len(dict_t)

    # Filter all the characters from s into a new list along with their index.
    # The filtering criteria is that the character should be present in t.
    filtered_s = []
    # 创建相关的fitered list进行滑动窗口
    for i, char in enumerate(s):
        if char in dict_t:
            filtered_s.append((i, char))
    #双指针进行遍历
    l, r = 0, 0
    formed = 0
    window_counts = {}

    ans = float("inf"), None, None
    # Look for the characters only in the filtered list instead of entire s. This helps to reduce our search.
    # Hence, we follow the sliding window approach on as small list.
    while r < len(filtered_s):
        character = filtered_s[r][1]
        window_counts[character] = window_counts.get(character, 0) + 1

        if window_counts[character] == dict_t[character]:
            formed += 1

        # If the current window has all the characters in desired frequencies i.e. t is present in the window
        while l <= r and formed == required:
            character = filtered_s[l][1]

            # Save the smallest window until now.
            end = filtered_s[r][0]
            start = filtered_s[l][0]
            if end - start + 1 < ans[0]:
                ans = (end - start + 1, start, end)

            window_counts[character] -= 1
            if window_counts[character] < dict_t[character]:
                formed -= 1
            l += 1    

        r += 1    
    return "" if ans[0] == float("inf") else s[ans[1] : ans[2] + 1]

2.滑动窗口的最大值

对一个给定的窗口，O(n^2)的算法就是直接求list的max值。

但是我们完全可以实现一个O(n)的算法，利用一个双向队列

当后面的值比前面的值大时，直接将前面的值pop出去

当后面的值比前面的值小时，保留下来

通过下标来判断是否目前的滑动窗口是否含有队列中最大值

from collections import deque
class Solution:
    def maxSlidingWindow(self, nums: 'List[int]', k: 'int') -> 'List[int]':
        # base cases
        n = len(nums)
        if n * k == 0:
            return []
        if k == 1:
            return nums
        
        def clean_deque(i):
            # remove indexes of elements not from sliding window
            if deq and deq[0] == i - k:
                deq.popleft()
                
            # remove from deq indexes of all elements 
            # which are smaller than current element nums[i]
            while deq and nums[i] > nums[deq[-1]]:
                deq.pop()
        
        # init deque and output
        deq = deque()
        max_idx = 0
        for i in range(k):
            clean_deque(i)
            deq.append(i)
            # compute max in nums[:k]
            if nums[i] > nums[max_idx]:
                max_idx = i
        output = [nums[max_idx]]
        
        # build output
        for i in range(k, n):
            clean_deque(i)          
            deq.append(i)
            output.append(nums[deq[0]])
        return output

2.3 分治算法

1.寻找两个有序数组的中位数

这道题如果时间复杂度没有限定在 O(log(m+n) 我们可以用 O(m+n) 的算法解决，用两个指针分别指向两个数组，比较指针下的元素大小，一共移动次数为 (m+n + 1)/2，便是中位数。

首先，我们理解什么中位数：指的是该数左右个数相等。

比如：odd : [1,2,3], 2 就是这个数组的中位数，左右两边都只要 1 位；

even: [1,2, 3,4]，2,3 就是这个数组的中位数，左右两边 1 位；

那么，现在我们有两个数组：

num1: [a1,a2,a3,…an]

nums2: [b1,b2,b3,…bn]

**[nums1[:left1],nums2[:left2]

nums1[left1:], nums2[left2:]]**

只要保证左右两边个数相同，中位数就在

这个边界旁边产生。

如何找边界值，我们可以用二分法，我们先确定 num1 取 m1 个数的左半边，那么 num2 取 m2 = (m+n+1)/2 - m1 的左半边，找到合适的 m1，就用二分法找。 [ [a1],[b1,b2,b3]

[a2,..an],[b4,…bn] ]

我们只需要比较 b3 和 a2 的关系的大小，就可以知道这种分法是不是准确的！

nums1 = [-1,1,3,5,7,9], nums2 =[2,4,6,8,10,12,14,16]

当 m1 = 4,m2 = 3,它的中位数就是median = (num1[m1] + num2[m2])/2

时间复杂度：O(log(min(m,n))）

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        n1 = len(nums1)
        n2 = len(nums2)
        if n1 > n2:
            return self.findMedianSortedArrays(nums2,nums1)
        k = (n1 + n2 + 1)//2
        left = 0
        right = n1
        while left < right :
            m1 = left +(right - left)//2
            m2 = k - m1
            if nums1[m1] < nums2[m2-1]:
                left = m1 + 1
            else:
                right = m1
        m1 = left
        m2 = k - m1 
        c1 = max(nums1[m1-1] if m1 > 0 else float("-inf"), nums2[m2-1] if m2 > 0 else float("-inf") )
        if (n1 + n2) % 2 == 1:
            return c1
        c2 = min(nums1[m1] if m1 < n1 else float("inf"), nums2[m2] if m2 <n2 else float("inf"))
        return (c1 + c2) / 2