ACM竞赛机试之五大常用算法
马上就要进行保研机试了,所以现在对最常用的ACM算法,根据体型进行总结,也算复习了一遍。
1. 枚举算法(Brute Force)
穷举法简单粗暴,没有什么问题是搞不定的,只要你肯花时间。同时对于小数据量,穷举法就是最优秀的算法。就像太祖长拳,简单,人人都能会,能解决问题,但是与真正的高手过招,就颓了。
下面介绍一些比较好用的优化和改进方法例题
1.1 立方质数问题
这道题完全就是一个暴力求解问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include<stdio.h>
#include<math.h>
#include <iostream>
using namespace std;
int isPrime(int number);
int main(){
int m; // 输入的整数
cin >> m;
if (m > 1000 || m < 1){
printf("输入数据不合法!");
return 0;
}
else
{
int flag = isPrime(m);
int t_flag = 0;
if (flag == 1){
int times = m % 3;
int k = m / 3;
for (int i = 2; i <m-4; i = i + 1){
for (int j = 2; j < m-i-1; j = j + 1 ){
if ((isPrime(i) == 1 && isPrime(j) == 1 && isPrime(m - i - j) == 1 && (i != j) && (i != (m - i - j)) && ((m - i - j) != j))
)
{
//cout << "Yes" << endl;
printf("Yes");
t_flag = 1;
return 1;
//break;
}
}
}
if (t_flag == 0){
//cout << "No" << endl;
printf("No");
}
//判断输入是否为素数
}
else {
//cout << "No" << endl;
printf("No");
}
//判断数据范围合法
}
return 1 ;
}
int isPrime(int number){
int flag=1;
int i; // 循环次数
int k; // m 的平方根
// 求平方根,注意sqrt()的参数为 double 类型,这里要强制转换m的类型
k = (int)sqrt((double)number);
for (i = 2; i <= k; i++){
if (number%i == 0){
flag = 0;
break;
}
}
return flag;
}
1.2 背包遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<iostream>
#include<stdio.h>
using namespace std;
#define LL long long
LL count1 = 0;
void dps(LL n, LL m, LL N, LL M, LL a[]) {
if (n > N || m > M)
return;
if (a[n] + m <= M)
{
if (n == N)
count1++;
else {
dps(n + 1, m, N, M, a);
m = m + a[n];
dps(n + 1, m, N, M, a);
}
}
else {
dps(n + 1, m, N, M, a);
}
}
int main()
{
LL n,m;
LL a[100];
cin >> n >> m;
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
dps(0, 0, n, m, a);
cout << count1;
return 0;
}
1.3 数组配对问题

将枚举对象变成对K的mod的排序,大大减少了计算量
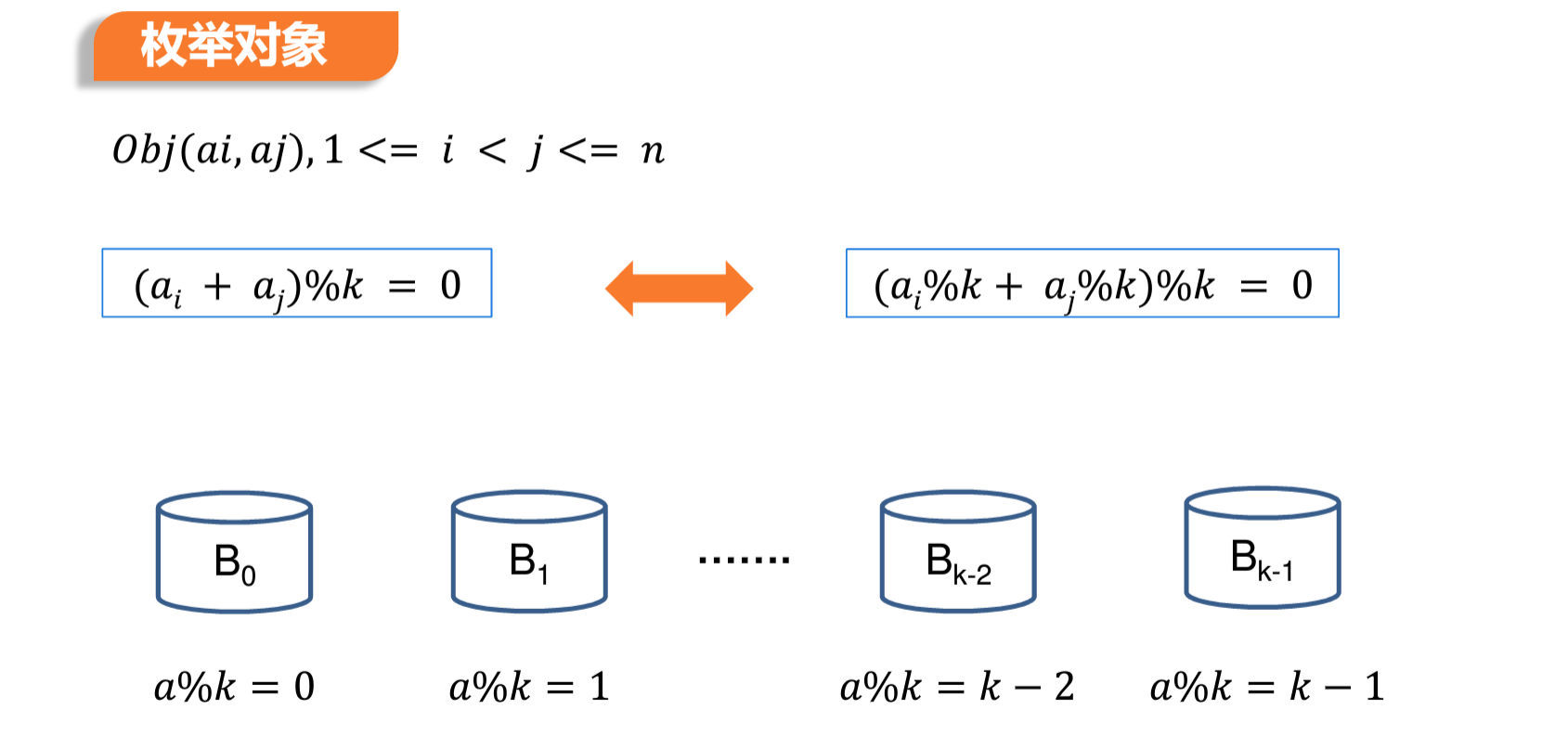
主要代码如下:

1.4 割绳子问题

首先先介绍一下二分查找算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/*
*二分查找思想:1、数组从小到大排序;2、查找的key每次和中间数比较,如果key小于mid
查找mid左侧的数组部分;如果key大于mid,则查找mid右侧的数组部分;如果相等,则直接返回mid。
输入:排序数组-array,数组大小-aSize,查找值-key
返回:返回数组中的相应位置,否则返回-1
*/
//非递归查找
int BinarySearch(int *array, int aSize, int key)
{
if ( array == NULL || aSize == 0 )
return -1;
int low = 0;
int high = aSize - 1;
int mid = 0;
while ( low <= high )
{
mid = (low + high )/2;
if ( array[mid] < key)
low = mid + 1;
else if ( array[mid] > key )
high = mid - 1;
else
return mid;
}
return -1;
}
//递归
int BinarySearchRecursive(int *array, int low, int high, int key)
{
if ( low > high )
return -1;
int mid = ( low + high )/2;
if ( array[mid] == key )
return mid;
else if ( array[mid] < key )
return BinarySearchRecursive(array, mid+1, high, key);
else
return BinarySearchRecursive(array, low, mid-1, key);
}
针对割绳子的问题,其实就是在寻找一个最大的长度,满足一定的条件p,因此我们就可以利用二分查找来做

1.5 石头移动问题
首先,针对这道题,它是一个枚举问题,我们需要对可以对所有的解法进行遍历,然后进行比较
也就是跟背包问题一致,是一个遍历问题,虽然利用0-1值描述了所有的方式,但是这样复杂度过高。
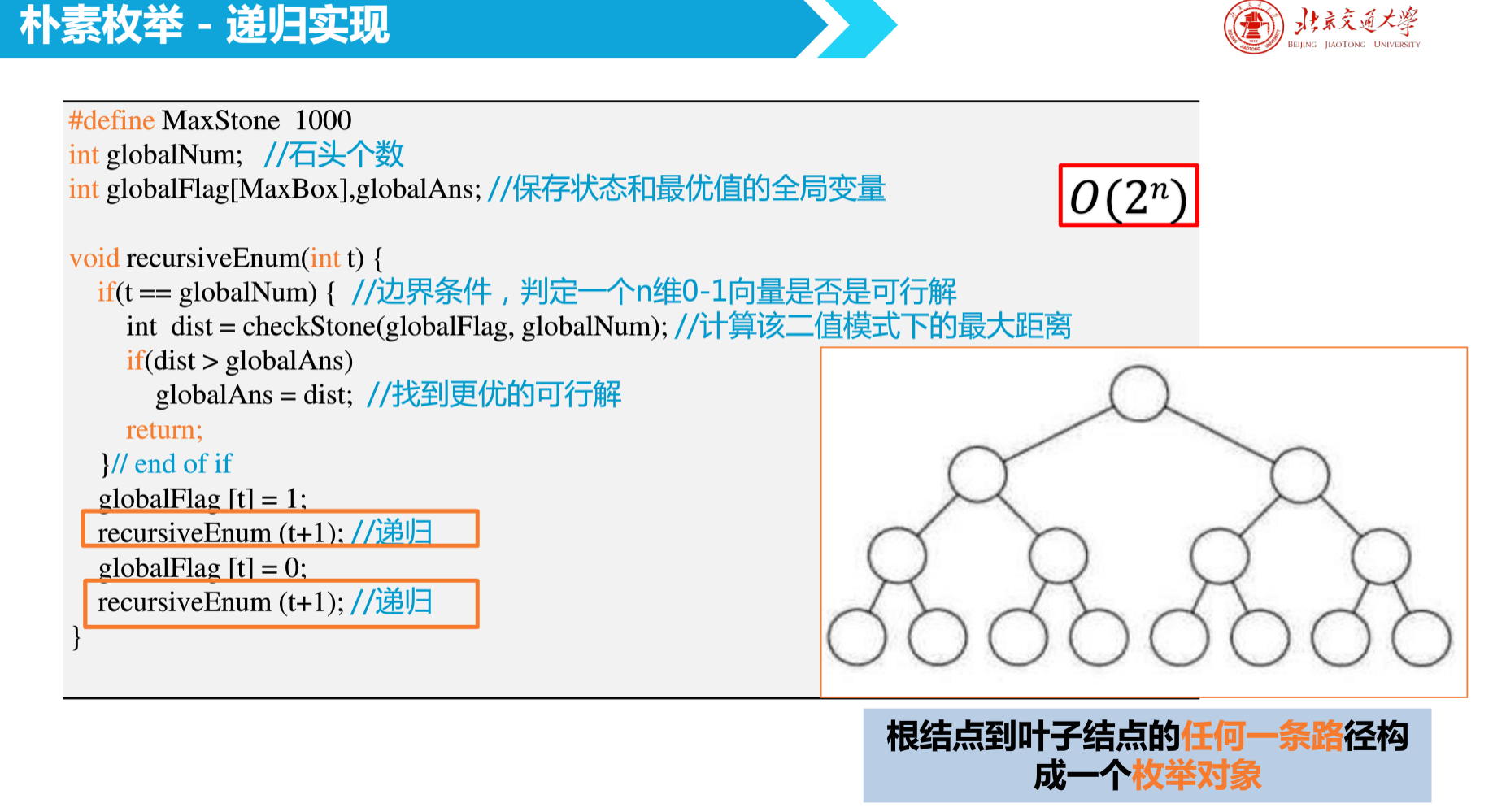
我们可以换种思路进行优化,这道题最后的输出是一个值,表示取出之后的最大值,那我们就可以将问题转化成利用二分法对这个最大值的求解,然后验证这个最大值是否有可行解,一次次二分就可以得到这个值。


1.6 数组排列最小值
题目:
输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。例如:输入数组{3,32,321},则打印出这3个数字能排成的最小数字321323
解题思路:
- 制定一种新的排序规则,数组根据这个规则排序之后能够排成一个最小的数字。
- 要制定新的排序规则,就必须制定新的比较规则,即通过比较m和n,来确定哪一个应该排在前面(即哪一个更“小”)
新的比较规则:
- 两个数字m和n能够拼接成为数字mn和nm,如果mn < nm,那么我们应该打印出mn,也就是m应该排在n之前,我们定义此时m < n;反之我们应该打印出nm,定义n < m;如果mn == nm,则定义m=n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
#include<stdio.h>
#include<algorithm>
using namespace std;
#define LL long long
bool compare(string a, string b)
{
string ab = a + b;
string ba = b + a;
return ab < ba;
}
int main()
{
int n;
cin >> n;
string a[100];
LL ans = 0;
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
sort(a, a + n, compare);
for (int i = 0; i < n; i++)
{
cout << a[i];
}
return 0;
}
2. 分治算法(Divide and Conquer)
这个算法的逻辑更简单了,就是一个词,分而治之。分治算法就是把一个大的问题分为若干个子问题,然后在子问题继续向下分,一直到base cases,通过base cases的解决,一步步向上,最终解决最初的大问题。分治算法是递归的典型应用。


2.1 合并排序和快速排序
先分,再合(一部分一部分的分合)

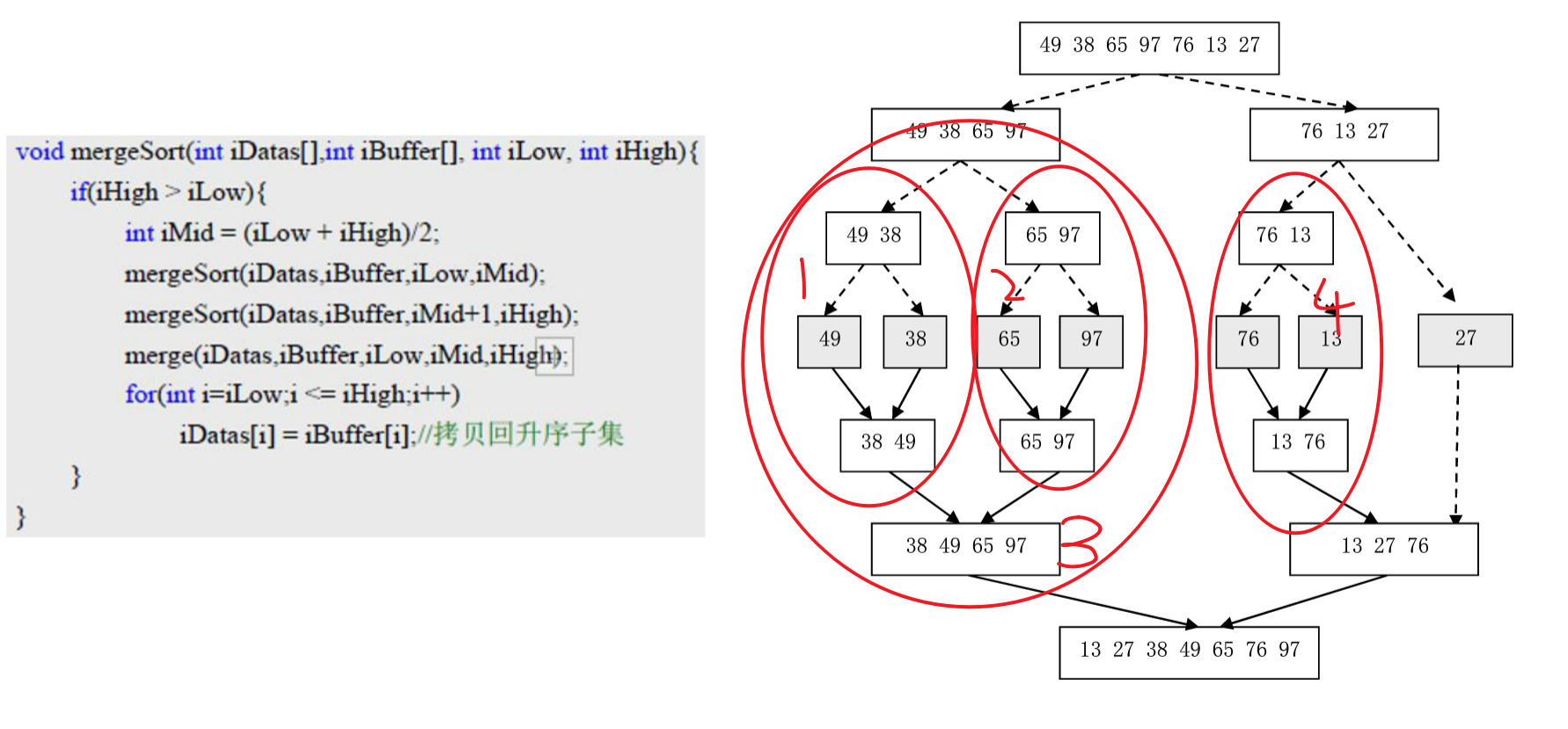
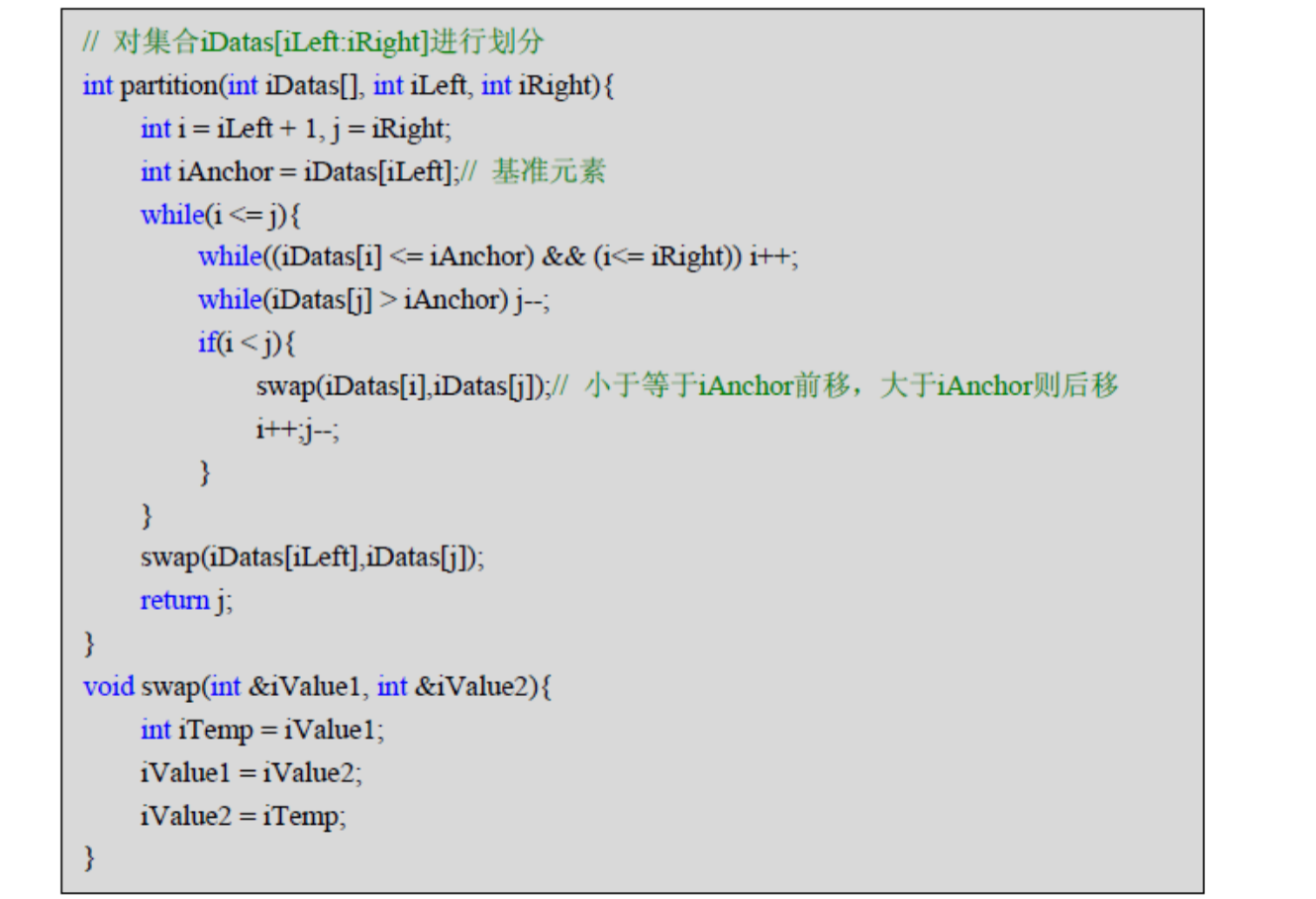
快速排序

线性时间(第7大数组)

2.2 逆序对数组

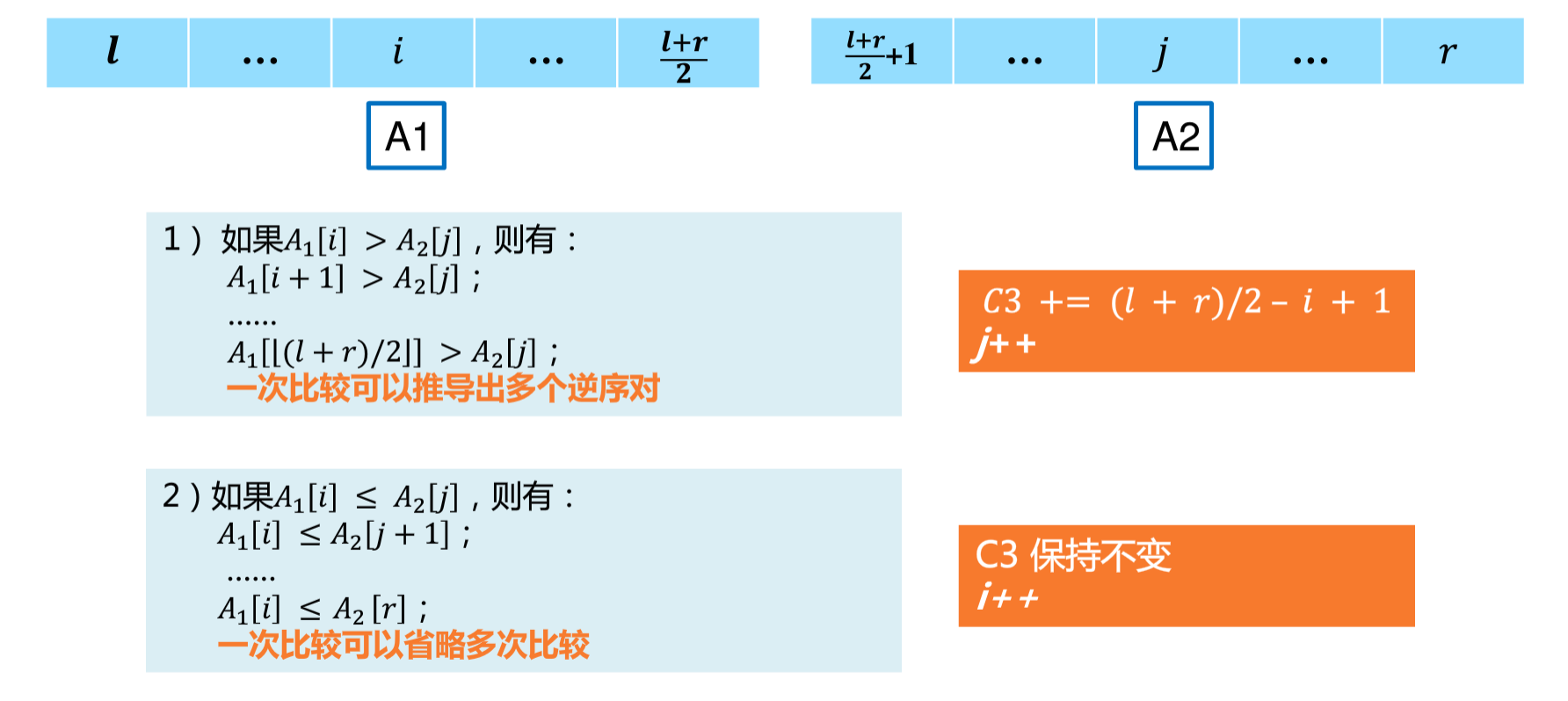


2.3 必胜问题
2.3.1 欧几里得的游戏
这道题还有点递归的味道,但是很多这种必胜的题目,都是在考找规律,显得特别难受,难上加难啊
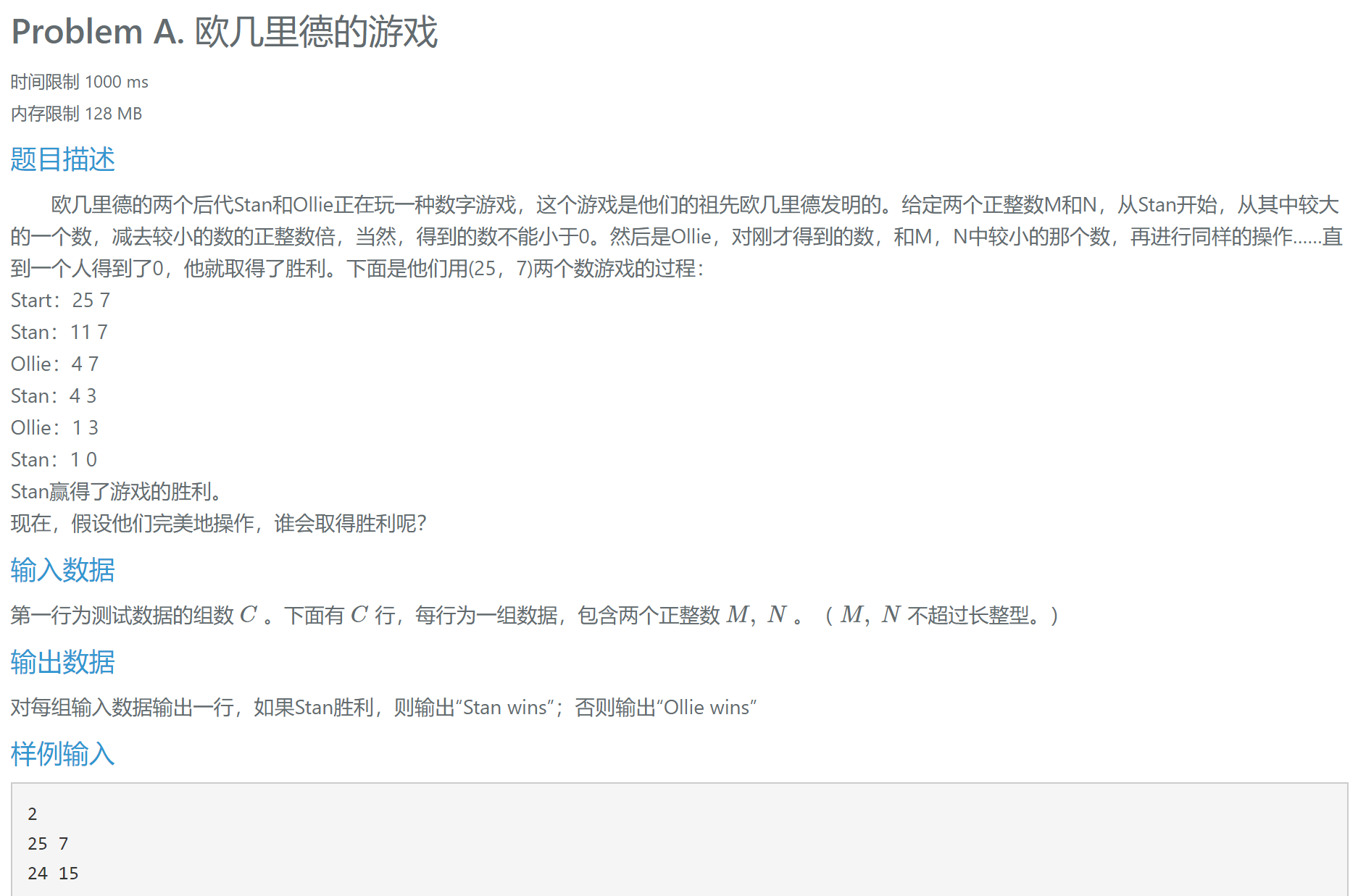
这里有三种情况 设给定的两个数字分别为 a ,b (a>=b)
1、a%b==0 谁面临这种情况谁就赢了
2、a<2*b 面临这种情况没有什么好挑的 只能用 a - b
3、a>2*b 这中情况就比较有意思了 当一个人面对这种情况时他就有了多种选择 因为他可以减去b的整数倍嘛 在这多种选择的情况下 某些选择最终会使他输掉而某些选择最终会使他赢 那到底该怎么选择是个很纠结的问题 一步走错满盘皆输嘛 但是我们不必纠结 因为题目中说 完美的操作 也就是说他会选择使自己赢的方法至于具体怎么选 我们就不用关心了 所以 谁面对这种情况 谁也就是赢的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int sum;
int flag;
void solve(LL a,LL b){
if (flag) return;
if(a<b) swap(a,b);
if (a%b==0||a>2*b){
flag=1,sum++;
return;
}
sum++;solve(a-b,b);
}
int main (){
int t;
scanf ("%d",&t);
while (t--){
LL a,b;
scanf ("%lld%lld",&a,&b);
sum=0;flag=0;
solve(a,b);
if (sum%2) printf ("Stan wins\n");
else printf ("Ollie wins\n");
}
return 0;
2.3.2 Easy Selection

这道题,谁先手谁就赢了!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
using namespace std;
//先取的人可以比较所有奇数位置数之和与所有偶数位置之和,哪个大就一直取相应的位置上的数....注意N为整数
//
//比如,6 1000 564 48 400 2
//
//奇数位置和为6+564+400=970 偶数位置和为1000+48+2=1050>970
//
//故先去的人可以先取2 后取的必定在奇数位置上取数(他只能取奇数位置的了)
//
//PS:先取的不一定是当前最优.......
int main()
{
int k,q;
scanf("%d",&k);
for(q=1;q<=k;q++)
{
int n,who;
int a;
scanf("%d\n%d\n",&n,&who);
for(int i=1;i<=n;i++)
{
scanf("%d",&a);
}
if(who==0)
printf("wind\n");
else
printf("lolanv\n");
}
return 0;
}
2.4 矩阵线性查找
要查找的元素与右上的元素比较,若比要查找的元素大,那这一列的元素都大可以排除,故将其左移;若小了,则排除这一行的元素,将其下移,每次都可以排除一列或一行的元素;最多m+n-1次就可以判断出是否存在
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
bool Find(int* matrix, int rows, int columns, int number)
{
if (matrix!=NULL && rows>0 && columns>0)
{
bool found = false;
int row = 0;
int column = columns-1;
while (row<rows && column>=0)
{
if (matrix[row * columns + column] == number)
{
found = true;
break;
}
else if(matrix[row * columns + column] > number)
column--;
else
row++;
}
return found;
}
}
3. 贪心算法
这部分算法说起来还算简单,就是根据一个策略进行层层深入。但是往往策略是比较难找到的
- 活动安排问题,寻找最早结束
- 小数背包问题,寻找利益比最高的进行收入
3.1 删数问题
3.1.1 保留最大数
题目:给出一个n位数,要求删掉其中k位数字,使得剩下的数字组成的数尽量大。
策略:利用两个指针对先对高位进行删除,如果高位小于次高位,删除高位,直到找到高位最大值;然后低位删除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <stdio.h>
#include <string.h>
#include <iostream>
#define mset(a,i) memset(a,i,sizeof(a))
using namespace std;
typedef long long ll;
const int MAX=1e6+5;
char a[MAX];
int vis[MAX];
int main()
{
int n,k,i,j;
while(cin>>n>>k)
{
scanf("%s",a);
int l=0,r=1;
mset(vis,0);
while(k&&r<n)//删升的
{
while(k&&l>=0&&a[l]<a[r])
{
vis[l]=1;
k--;
while(l>=0&&vis[l])l--;
}
l=r;r++;
}
r=n-1;
while(k&&r>=0){//扫描剩下的不升序列
if(!vis[r]){
vis[r]=1;
k--;
}
r--;
}
int flag=1;
for(int i=0;i<n;i++)
{
if(!vis[i]){
flag=0;
printf("%c",a[i]);
}
}
if(flag)printf("0");
puts("");
}
return 0;
}
3.1.2 保留最小数
题目:给出一个n位数,要求删掉其中k位数字,使得剩下的数字组成的数尽量小。
最优解是删除出现的第一个左边>右边的数,因为删除之后高位减小,很容易想…那全局最优解也就是这个了,因为删除S个数字就相当于执行了S次删除一个数,因为留下的数总是当前最优解…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def solution(num, k):
s = str(num)
flag = True
while k:
for i in range(len(s)-1):
#每次删除第一个比下一个数字大的数
if s[i] > s[i+1]:
s = s.replace(s[i],'',1)
flag = False
break
#如果所有数字递增,则删除最后几个数字直接返回
if flag:
s = s[:len(s)-k]
k -= 1
return int(s)
3.2 哈夫曼编码变形
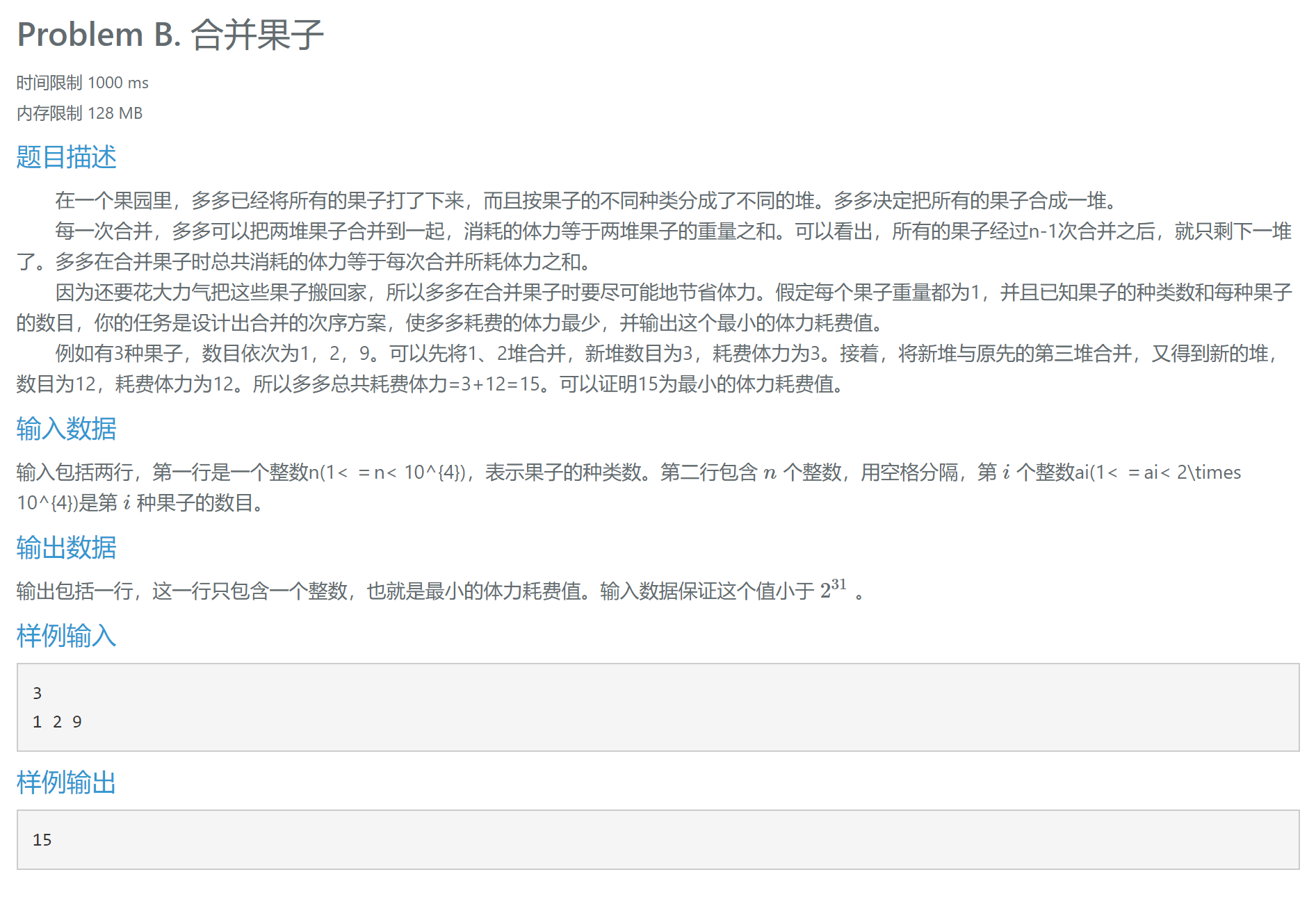
每次都拿最小的两个进行合并,然后将结果添加进去。
这里使用STL库中的优先队列,priority_queue<int, vector<int>, greater<int> > q;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<iostream>
#include<algorithm>
#include<stdio.h>
#include<queue>
using namespace std;
int main()
{
int n;
int i;
cin >> n;
int a,b;
priority_queue<int, vector<int>, greater<int> > q;
for (i = 0; i < n; i++) {
cin >> a;
q.push(a);
}
if (n == 1) {
cout << 0;
return 0;
}
int c=0;
for (i = 0; i < n - 1; i++) {
a = q.top();
q.pop();
b = q.top();
q.pop();
b = a + b;
q.push(b);
c += b;
}
//a = q.top();
cout << c;
//system("pause");
return 0;
}
3.3 最小差距
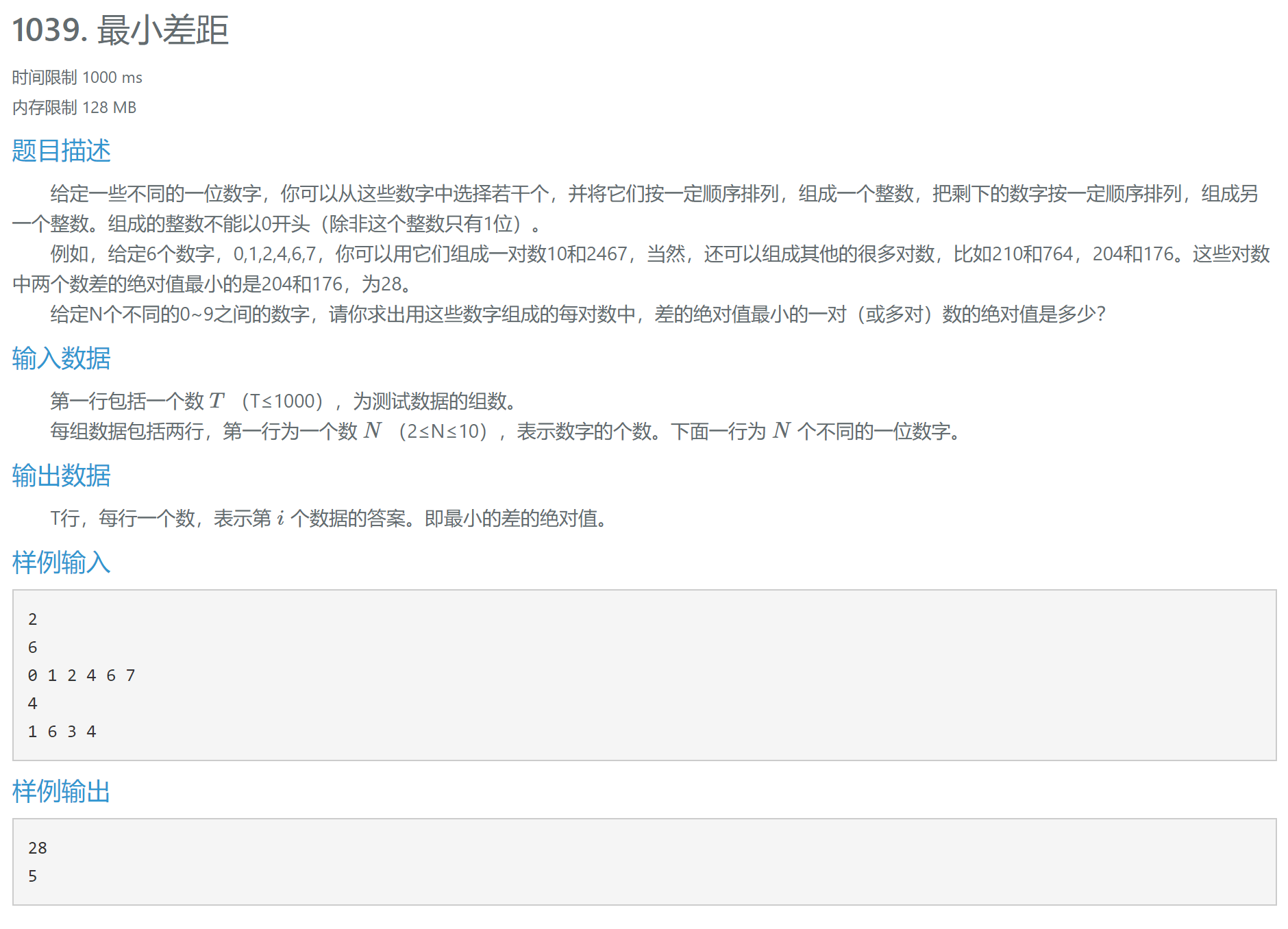
【分析】 首先想到的算法是暴力穷举,但是时间复杂度无法承受。于是我们考虑贪心策略。 首先把这N个数降序排列,这一点应该不用解释了。接下来分类讨论:
- 对于第一种情况,不难想到这样的贪心策略:将最小的非0数字作为x的最高位,然后依次从左往右取k位加入x,从右往左取k位作为y,x-y的绝对值即为答案。
- 对于第二种情况,稍微复杂些:枚举非零数字a[i]作为x的最高位,a[i+1]作为y的最高位,从右往左取k-1位加入x,从左往右取k-1位加入y,打擂台更新答案。
- 对于第三种情况,特判输出。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
using namespace std;
int a[15];
int n;
int abs(int x){ return (x<0?-x:x); }
int work1(){
if (a[1]==0) swap(a[1],a[2]);
int s1=0,s2=0;
for (int i=1;i<=n/2+1;i++) s1=s1*10+a[i];
for (int i=n;i>=n/2+2;i--) s2=s2*10+a[i];
return abs(s1-s2);
}
int work2(){
int book[15];
int s1,s2;
int ans=(1<<31)-1;
for (int i=2;i<=n;i++)
if (a[i-1]){
s1=a[i],s2=a[i-1];
memset(book,0,sizeof(book));
book[i]=book[i-1]=1;
int l=1,r=n;
for (int j=1;j<=(n-2)/2;j++){
while (book[l]) l++;
while (book[r]) r--;
book[l]=book[r]=1;
s1=s1*10+a[l];s2=s2*10+a[r];
}
ans=min(ans,abs(s1-s2));
}
return ans;
}
int main(){
int t;
cin>>t;
while (t--){
scanf("%d",&n);
for (int i=1;i<=n;i++) scanf("%d",&a[i]);
sort(a+1,a+1+n);
if (n==2) { printf("%d\n",a[2]-a[1]);continue; }
if (n%2==1) printf("%d\n",work1()); else printf("%d\n",work2());
}
}
3.4 上帝的游戏

这道题就是在寻找,数字对数,如果有4个 那就有一对,如果有2,2也算一对
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
using namespace std;
int cnt[4000] = {0};
int N;
void setEmpty(){
for(int i = 0;i < N;i++)
cnt[i] = 0;
}
int main(){
int num = 0;
cin>>N;
bool flag = false;
int x;
for(int i = 0;i < N;i++){
cin>>x;
cnt[x]++;
if(cnt[x] == 4 || (cnt[x] == 2 && flag == true)){
setEmpty();
//cout<<x<<endl;
num++;
flag = false;
}
else if(cnt[x] == 2 && flag == false){
flag = true;
}
}
cout<<num;
return 0;
}
3.5 多点种植问题
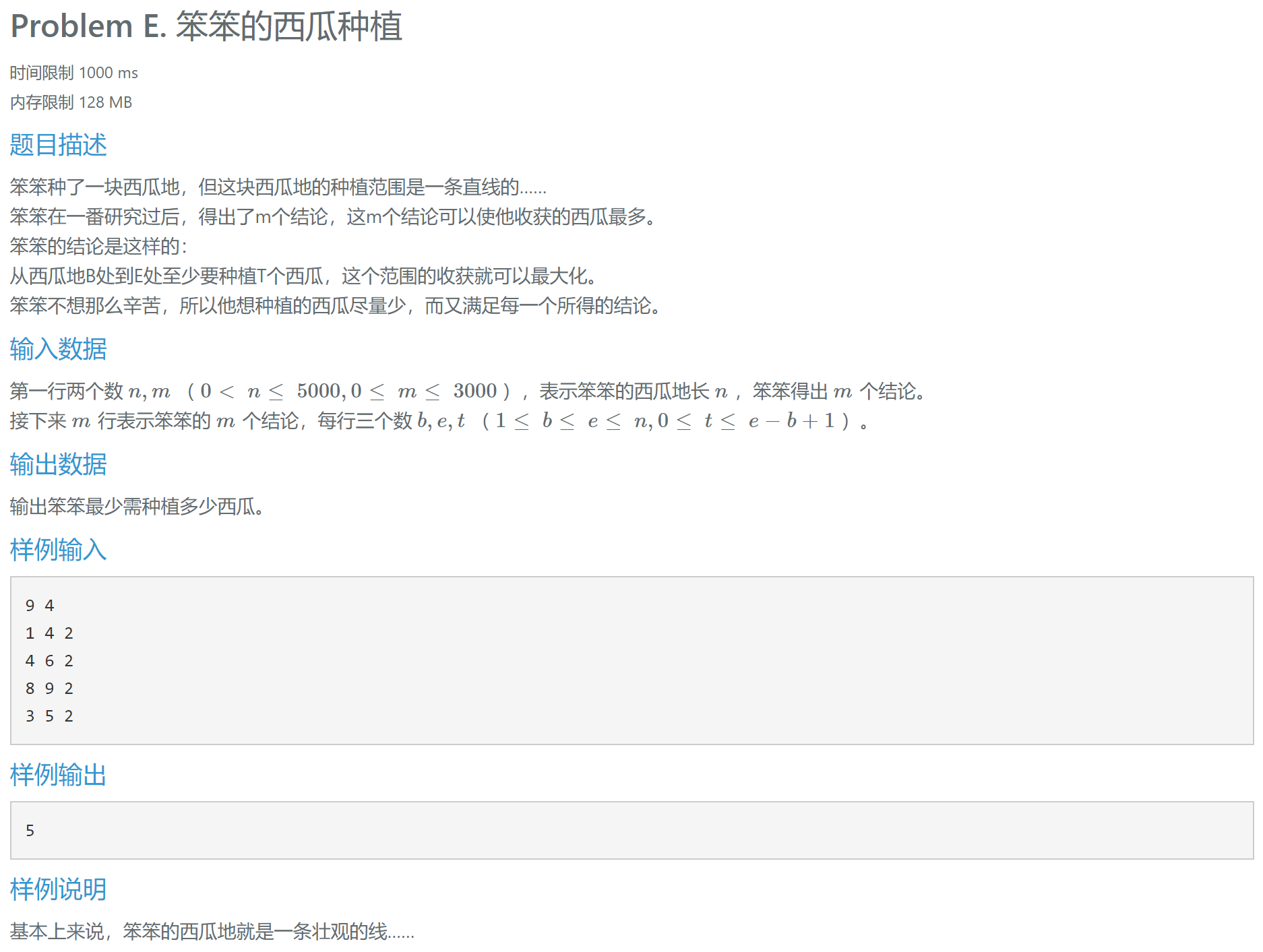
本题的贪心策略为尽量往右边边界种,首先将规则进行排序,按照从左往右的形式进行排列,然后再进行安插
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<stack>
#include<queue>
using namespace std;
struct ill{
int l,r,g;
}a[3001];
bool fuu(ill x,ill y)
{
if(x.r<y.r)
return 1;
if(x.r==y.r&&x.l<y.l)
return 1;
return 0;
}
int v[5001],k;
int main()
{
int n,m,i,j;
scanf("%d%d",&n,&m);
for(i=0;i<m;i++)
scanf("%d%d%d",&a[i].l,&a[i].r,&a[i].g);
sort(a,a+m,fuu);
for(i=0;i<m;i++)
{
for(j=a[i].l;j<=a[i].r;j++)
if(v[j])
a[i].g--;
if(a[i].g>0)
{
for(j=a[i].r ; j>=a[i].l&&a[i].g>0 ; j--)
{
if(!v[j])
{
v[j]=1;
a[i].g--;
}
}
}
}
for(i=0;i<=n;i++)
if(v[i])
k++;
printf("%d",k);
}
4. 动态规划
这一章节,按以往经验来说应该算比较难的,跟贪心的策略一样,递推方程的确不好推导出来。
但是这种方法往往很常用,也很容易被考察。
4.1 0-1 背包

4.2 路径权重问题
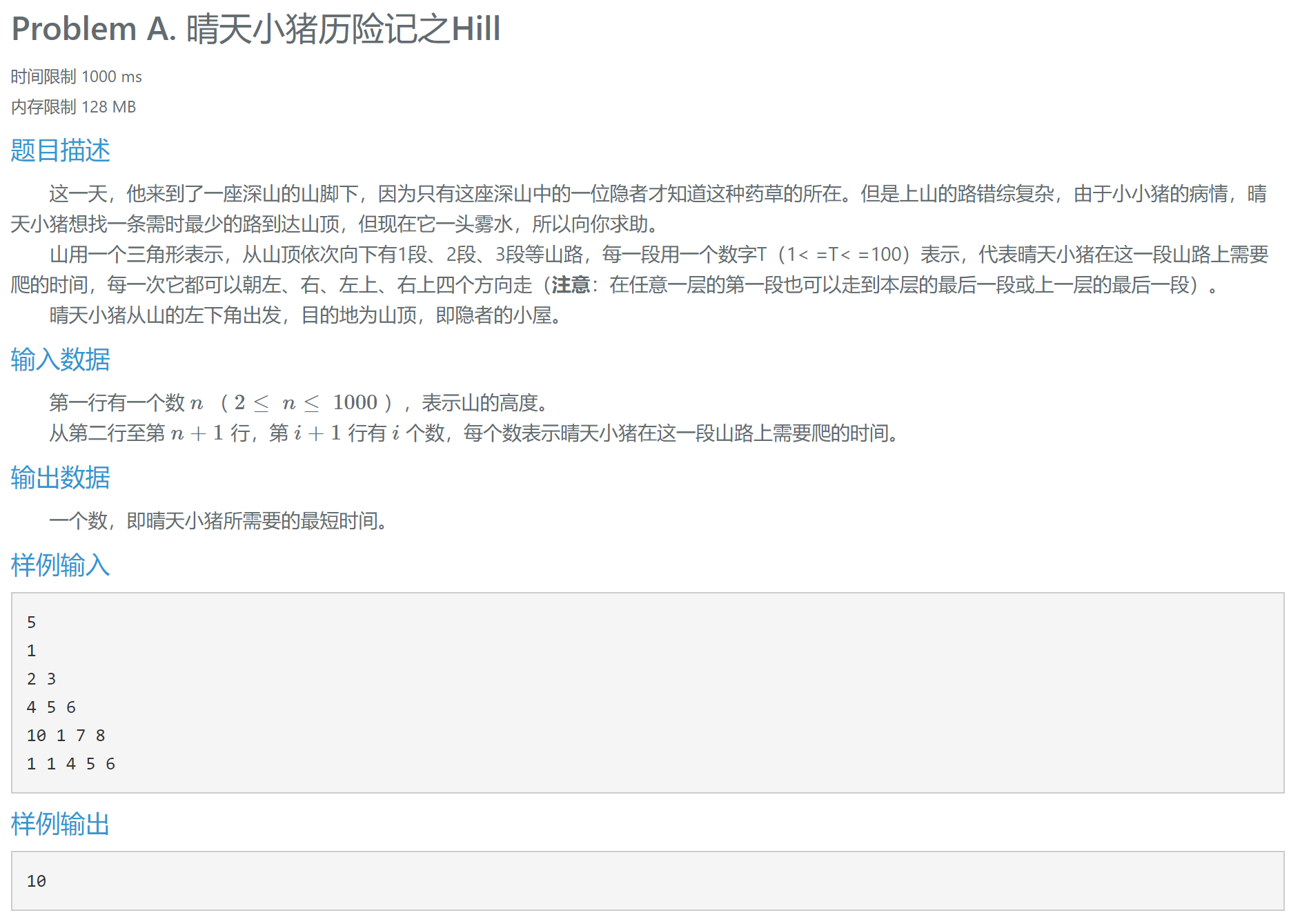
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 1005;
int a[maxn][maxn];
int f[maxn][maxn];
int n;
int main()
{
int i ,j;
cin >> n;
for (i = 1; i <= n; i++)
{
for (j = 1; j <= i; j++)
cin >> a[i][j];
}
f[1][1] = a[1][1];
for (i = 2; i <= n; i++)
{
for(int j = 2; j<i; j++)//先求出从上一层推出来的最小值
f[i][j] = min(f[i - 1][j], f[i - 1][j - 1]) + a[i][j];
f[i][1] = min(f[i - 1][1], f[i - 1][i - 1]) + a[i][1];//特殊边界点处理
f[i][i] = min(f[i - 1][i - 1], f[i - 1][1]) + a[i][i];//特殊边界点处理
//同一层更新最优解
for (int k = i - 1; k>0; k--)//从右往左推 从右往左走的情况更新
f[i][k] = min(f[i][k], f[i][k + 1] + a[i][k]);
f[i][i] = min(f[i][i], f[i][1] + a[i][i]);
for (int l = 2; l <= i; l++)//从左往右推 从左往右走的情况更新
f[i][l] = min(f[i][l], f[i][l - 1] + a[i][l]);
f[i][1] = min(f[i][1], f[i][i] + a[i][1]);
for (int k = i - 1; k>0; k--)//再推一遍从右往左推 从右往左走的情况更新
f[i][k] = min(f[i][k], f[i][k + 1] + a[i][k]);
f[i][i] = min(f[i][i], f[i][1] + a[i][i]);
for (int l = 2; l <= i; l++)//再推一遍从左往右推 从左往右走的情况更新
f[i][l] = min(f[i][l], f[i][l - 1] + a[i][l]);
f[i][1] = min(f[i][1], f[i][i] + a[i][1]);
}
cout << f[n][1] << endl;
return 0;
}
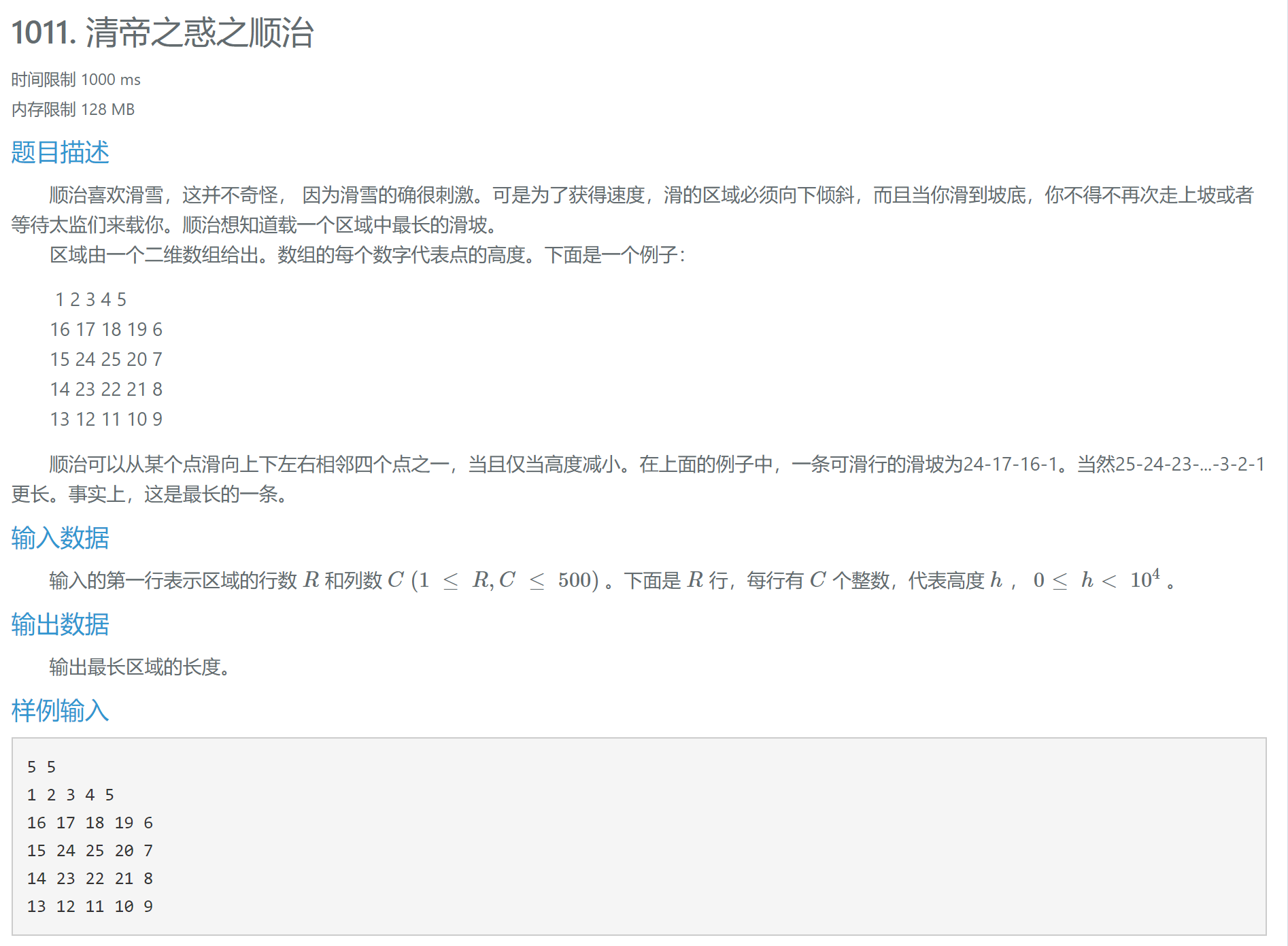
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <cstring>
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int ans[502][502]={0},table[502][502]={0},n,u=0,m;
int dfs(int x,int y)
{
if(ans[x][y])
return ans[x][y];
ans[x][y]=1;
if(x!=0&&table[x][y]>table[x-1][y])
ans[x][y]=dfs(x-1,y)+1;
if(y!=0&&table[x][y]>table[x][y-1])
ans[x][y]=max(dfs(x,y-1)+1,ans[x][y]);
if(x!=n-1&&table[x][y]>table[x+1][y])
ans[x][y]=max(dfs(x+1,y)+1,ans[x][y]);
if(y!=m-1&&table[x][y]>table[x][y+1])
ans[x][y]=max(dfs(x,y+1)+1,ans[x][y]);
return ans[x][y];
}
int main()
{
cin>>n>>m;
for(int i=0;i!=n;i++)
for(int j=0;j!=m;j++)
cin>>table[i][j];
for(int i=0;i!=n;i++)
for(int j=0;j!=m;j++)
u=max(u,dfs(i,j));
cout<<u<<endl;
}
5. 搜索算法
具体可以说有五种(A*不常用)
- DPS深度
- BPS广度
- 回溯算法 利用限界函数来剪支的DPS
- 分支限界法 利用限界函数来剪支的BPS
- 启发式搜索 利用状态估计函数,来估计最优
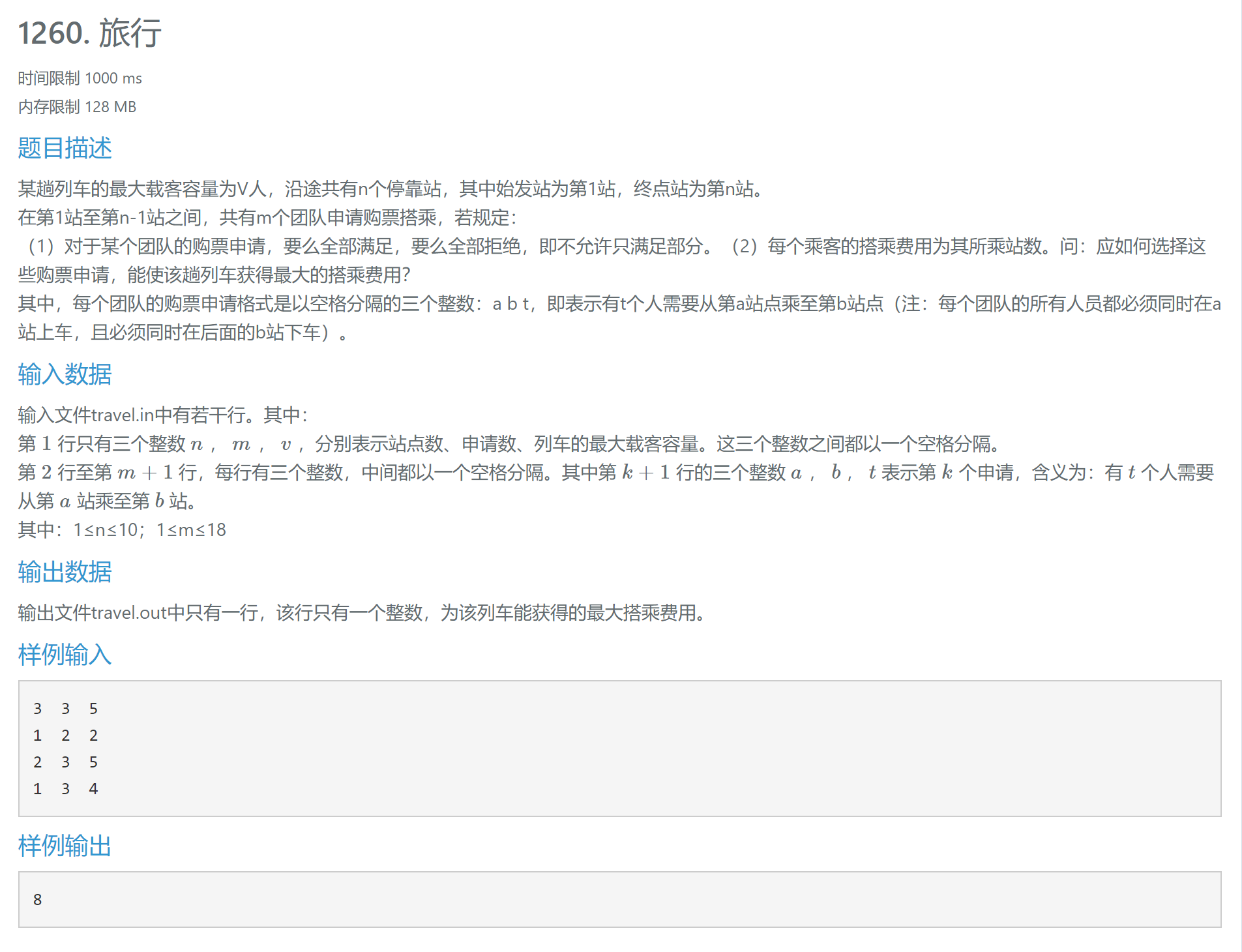
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<iostream>
#define maxn 19
int n,m,v,ans;
int chafen[maxn],a[maxn],b[maxn],t[maxn];
bool exsit[maxn];
using namespace std;
//判定
bool cheak(){
int total=0;
for(int i=1; i<=n; i++)
{
total+=chafen[i];
if(total>v)return 0;
}
return 1;
}
void dfs(int dep)
{
if(dep==m+1) {
for(int i=1; i<=n; i++) chafen[i]=0; //初始化
int temp=0;
for(int i=1; i<=m; i++)
if(exsit[i]) {
chafen[a[i]]+=t[i];
chafen[b[i]]-=t[i];
temp+=(b[i]-a[i])*t[i];
}
if(cheak())ans=max(ans,temp);
return;
}
dfs(dep+1);
exsit[dep]=1;
dfs(dep+1);
exsit[dep]=0;
}
int main()
{
cin>>n>>m>>v;
for(int i=1; i<=m; i++)
{
cin>>a[i]>>b[i]>>t[i];
}
dfs(1);
cout<<ans<<endl;
}